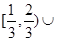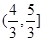题目内容
已知函数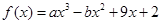 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的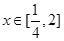 ,都有f(x)
,都有f(x)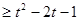 成立,求函数g(t)
成立,求函数g(t)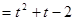 的最值
的最值
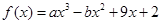 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的
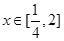 ,都有f(x)
,都有f(x)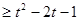 成立,求函数g(t)
成立,求函数g(t)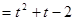 的最值
的最值答:① ;②t=
;②t= 最小值
最小值 ,t=3最大值10。
,t=3最大值10。
 ;②t=
;②t= 最小值
最小值 ,t=3最大值10。
,t=3最大值10。试题分析:答:①
 ,
,
 ………2分
………2分 ………4分
………4分②列表如下:
 |  |  |  |  |  |  | 2 |
 | | + | 0 | - | 0 | + | |
 |  |    |  |  |  |   | 4 |
 =2 8分
=2 8分对任意的
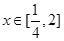 都有f(x)
都有f(x)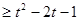 成立,
成立,f(x)
 ="2"
="2" 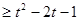 ,
,  10分
10分g(t)
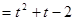 (
( ),
), t=
 最小值
最小值 ,t=3最大值10 12分
,t=3最大值10 12分点评:中档题,此类问题较为典型,是导数应用的基本问题。在某区间,导函数值非负,函数为增函数,导函数值非正,函数为减函数。求最值应遵循“求导数,求驻点,计算极值及端点函数值,比较确定最值”。不等式恒成立问题,往往通过构造函数,研究函数的最值,使问题得到解决。本题利用“表解法”,清晰、直观、易懂。

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目




 和
和 (其中
(其中 ),
), 与函数
与函数 的图像从左至右相交于点
的图像从左至右相交于点 ,
, ,
, 与函数
与函数 ,
, .记线段
.记线段 和
和 在
在 轴上的投影长度分别为
轴上的投影长度分别为 .当
.当 变化时,
变化时, 的最小值为( )
的最小值为( )



 ,
, ,求
,求 的范围; (2)不等式
的范围; (2)不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
 .
.  时取得极值?说明理由;
时取得极值?说明理由; ,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.  ,g(x)=
,g(x)= ,a,b∈R.
,a,b∈R. .
.  ;
;  ,求证:
,求证: ≤
≤ .
.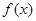 是定义在
是定义在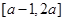 上的偶函数,且当
上的偶函数,且当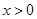 时,
时,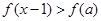 的解集为 ( )
的解集为 ( )