题目内容
设cos2θ=
,则cos4θ+sin4θ的值是 .
| ||
| 3 |
分析:由cos2θ=
,再根据根据同角三角函数的基本关系、二倍角公式求得cos4θ+sin4θ的值.
| ||
| 3 |
解答:解:由于cos2θ=
,
则cos4θ+sin4θ=(sin2θ+cos2θ)2-2sin2θcos2θ
=1-
sin22θ=1-
(1-cos22θ)=1-
(1-
)=
,
故答案为:
.
| ||
| 3 |
则cos4θ+sin4θ=(sin2θ+cos2θ)2-2sin2θcos2θ
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 9 |
| 11 |
| 18 |
故答案为:
| 11 |
| 18 |
点评:本题主要考查同角三角函数的基本关系的应用,二倍角公式的应用,属于中档题.

练习册系列答案
相关题目
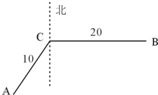 如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.
如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.