题目内容
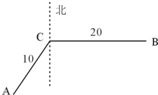 如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.
如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.(1)求A船与B船间的距离.
(2)设A船沿直线方向前往B处,其方向与
| AB |
| 3 |
| π |
| 4 |
分析:(1)在△ABC中,由已知得到:∠BCA=120°,BC=20,AC=10,再由余弦定理得AB的长,即A船与B船间的距离;
(2)在△ABC中,先由正弦定理得角A的正弦值,从而得出f(x)的表达式,再利用二倍角公式化成:2
cos(2x+
)+
的形式,最后利用三角函数的性质救是值域,单调减区间即可.
(2)在△ABC中,先由正弦定理得角A的正弦值,从而得出f(x)的表达式,再利用二倍角公式化成:2
| 3 |
| π |
| 6 |
| 3 |
解答:解:(1)在△ABC中,已知∠BCA=120°,BC=20AC=10由余弦定理得:AB2=BC2+AC2-2BC•AC•cos20°=700,∴AB=10
即A船与B船间的距离为10
n,mil(4分)
(2)在△ABC中,由正弦定理得
=
,即
=
∴sim?=
(7分)
f(x)=7×
cos2x+2
•
=3cos2x+
-
sin2x=2
cos(2x+
)+
(9分)
故值域[-
,,3
],单调减区间为[kπ-
,kπ+
]k∈z(12分)
| 7 |
即A船与B船间的距离为10
| 7 |
(2)在△ABC中,由正弦定理得
| BC |
| sim? |
| AB |
| sim120° |
| 20 |
| sim? |
10
| ||
| sim120° |
∴sim?=
| ||
| 7 |
f(x)=7×
| 3 |
| 7 |
| 3 |
1+cos(2x+
| ||
| 2 |
=3cos2x+
| 3 |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
故值域[-
| 3 |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
点评:本题主要考查了解三角形的实际应用.解题的关键是利用了余弦定理,利用已知的边和角建立方程求得距离.

练习册系列答案
相关题目
 如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深BE=200 m,于C处测得水深CF=110 m,求∠DEF的余弦值.
如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深BE=200 m,于C处测得水深CF=110 m,求∠DEF的余弦值.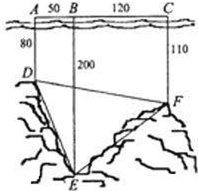 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,求∠DEF的余弦值.
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,求∠DEF的余弦值.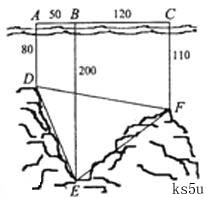 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知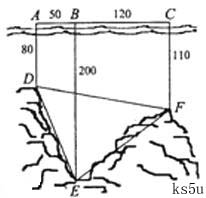 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知