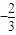题目内容
设sinα+sinβ=
,则sinα-cos2β,的最大值为( )
| 1 |
| 3 |
分析:根据所给的函数式,整理出sinβ=(
-sinα),代入要求的三角函数式,整理出关于sinα的二次函数形式,根据正弦函数的值域,得到函数的最大值.
| 1 |
| 3 |
解答:解:∵sinα+sinβ=
sinβ=(
-sinα)
sinα-cos2β
=sinα-1+(sinβ)2
=sinα-1+(
-sinα)2
=(sinα)2+
sinα-
=(sinα+
)2-
∴当sinα=1时,上式取最大值=
故选B.
| 1 |
| 3 |
sinβ=(
| 1 |
| 3 |
sinα-cos2β
=sinα-1+(sinβ)2
=sinα-1+(
| 1 |
| 3 |
=(sinα)2+
| 1 |
| 3 |
| 8 |
| 9 |
=(sinα+
| 1 |
| 6 |
| 11 |
| 12 |
∴当sinα=1时,上式取最大值=
| 4 |
| 9 |
故选B.
点评:本题考查三角函数的化简求值即二次函数的性质,本题解题的关键是整理出关于正弦函数的二次函数的形式,问题转化成二次函数的最值.

练习册系列答案
相关题目
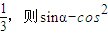 β,的最大值为( )
β,的最大值为( )