题目内容
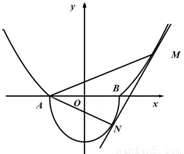
 如图所示的曲线C是由部分抛物线C 1:y=x2-1(|x|≥1)和曲线C2:x2+
如图所示的曲线C是由部分抛物线C 1:y=x2-1(|x|≥1)和曲线C2:x2+| y2 |
| m |
(1)当t=
| 2 |
(2)当实数m取何值时,∠MAB=∠NAB?并求出此时直线l的方程.
分析:(1)依题意可表示出切线的方程整理后代入C2的方程整理求得m的关系式,利用判别式等于0,即可求得m的值,从而可得N的坐标;
(2)题意可表示出切线的方程整理后代入C2的方程整理求得m的关系式,利用判别式等于0,即可求得m=0或m和t的关系式,表示出直线AM和AN的斜率,若∠MAB=∠NAB,则kAM=-kAN,求得t,进而根据中m和t的关系式,求得m,进而求得M,N的坐标,利用两点式求得MN所在直线的方程.
(2)题意可表示出切线的方程整理后代入C2的方程整理求得m的关系式,利用判别式等于0,即可求得m=0或m和t的关系式,表示出直线AM和AN的斜率,若∠MAB=∠NAB,则kAM=-kAN,求得t,进而根据中m和t的关系式,求得m,进而求得M,N的坐标,利用两点式求得MN所在直线的方程.
解答:解:(1)切线l:y-1=2
(x-
),即y=2
x-3,
代入x2+
=1,化简并整理得(m+8)x2-12
x+9-m=0,
由△=(12
)2+4(m+8)(9-m)=4m(m-1)=0
∵m>0,∴m=1.
此时,点N的坐标为(
,-
).
(2)由题意可知M(t,t2-1),切线l的方程表达式为y-(t2-1)=2t(x-t),即y=2tx-t2-1,
与x2+
=1联立方程组,整理得(m+4t2)x2-4t(t2+1)x+(t2+1)2-m=0,(*)
由△=16t2(t2+1)2+4(m+4t2)[m-(t2+1)2]=4m[m-(t2-1)2]=0
得m=0(舍去)或m=(t2-1)2.
此时,点N的坐标为(
,-
).
∵A(-1,0),M(t,t2-1),∴kAM=
=t-1,kAN=
=-(t-1)2,
若∠MAB=∠NAB,则kAM=-kAN,即t=2,此时m=9,
故当实数m=9时,∠MAB=∠NAB.
此时kAM=1,kAN=-1,∠MAB=∠NAB=45°,
∴M(2,3),N(
,-
),
∴MN所在直线的方程为y=4x-5.
| 2 |
| 2 |
| 2 |
代入x2+
| y2 |
| m |
| 2 |
由△=(12
| 2 |
∵m>0,∴m=1.
此时,点N的坐标为(
2
| ||
| 3 |
| 1 |
| 3 |
(2)由题意可知M(t,t2-1),切线l的方程表达式为y-(t2-1)=2t(x-t),即y=2tx-t2-1,
与x2+
| y2 |
| m |
由△=16t2(t2+1)2+4(m+4t2)[m-(t2+1)2]=4m[m-(t2-1)2]=0
得m=0(舍去)或m=(t2-1)2.
此时,点N的坐标为(
| 2t |
| t2+1 |
| (t2-1)2 |
| t2+1 |
∵A(-1,0),M(t,t2-1),∴kAM=
| t2-1 |
| t+1 |
-
| ||
|
若∠MAB=∠NAB,则kAM=-kAN,即t=2,此时m=9,
故当实数m=9时,∠MAB=∠NAB.
此时kAM=1,kAN=-1,∠MAB=∠NAB=45°,
∴M(2,3),N(
| 4 |
| 5 |
| 9 |
| 5 |
∴MN所在直线的方程为y=4x-5.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题的能力,推理计算能力,知识的综合问题.

练习册系列答案
相关题目
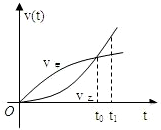 已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )| A、在t1时刻,甲车在乙车前面 | B、t1时刻后,甲车在乙车后面 | C、在t0时刻,两车的位置相同 | D、t0时刻后,乙车在甲车前面 |
 2、有一空容器,由悬在它上方的一根水管均匀地注水,直至把容器注满,在注水过程中水面的高度变化曲线如图所示,其中PQ为一线段,则与此图相对应的容器的形状是( )
2、有一空容器,由悬在它上方的一根水管均匀地注水,直至把容器注满,在注水过程中水面的高度变化曲线如图所示,其中PQ为一线段,则与此图相对应的容器的形状是( ) 12、某次我市高三教学质量检测中,甲、乙、丙三科考试成绩的直方图如如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由如图曲线可得下列说法中正确的一项是( )
12、某次我市高三教学质量检测中,甲、乙、丙三科考试成绩的直方图如如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由如图曲线可得下列说法中正确的一项是( )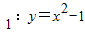 (|x|≥1)和曲线C2:
(|x|≥1)和曲线C2: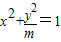 (y≤0,m>0)“合成”的,直线l与曲线C1相切于点M,与曲线C2相切于点N,记点M的横坐标为t(t>1),其中A(-1,0),B(1,0).
(y≤0,m>0)“合成”的,直线l与曲线C1相切于点M,与曲线C2相切于点N,记点M的横坐标为t(t>1),其中A(-1,0),B(1,0). 时,求m的值和点N的坐标;
时,求m的值和点N的坐标;