题目内容
已知椭圆 +
+ =1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
=1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆 +
+ =1(a>b>0)的离心率为 .
=1(a>b>0)的离心率为 .
 +
+ =1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
=1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆 +
+ =1(a>b>0)的离心率为 .
=1(a>b>0)的离心率为 .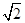 -1
-1抛物线y2=2px(p>0)的焦点坐标为(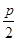 ,0),
,0),
由题意知,椭圆的半焦距c=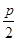 ,
,
又当x=c时,由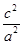 +
+ =1得y2=
=1得y2=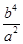 ,
,
∴|PQ|=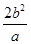 ,
,
由P、Q在抛物线上且PQ过点F,
∴|PQ|=2p.
∴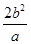 =2p,b2=ap.
=2p,b2=ap.
又a2=b2+c2,
即a2=ap+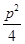 ,
,
解得a=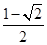 p(舍)或a=
p(舍)或a=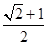 p.
p.
∴e=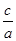 =
=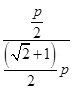 =
=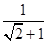 =
=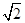 -1.
-1.
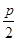 ,0),
,0),由题意知,椭圆的半焦距c=
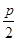 ,
,又当x=c时,由
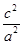 +
+ =1得y2=
=1得y2=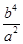 ,
,∴|PQ|=
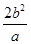 ,
,由P、Q在抛物线上且PQ过点F,
∴|PQ|=2p.
∴
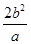 =2p,b2=ap.
=2p,b2=ap.又a2=b2+c2,
即a2=ap+
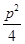 ,
,解得a=
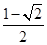 p(舍)或a=
p(舍)或a=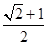 p.
p.∴e=
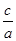 =
=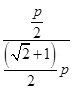 =
=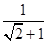 =
=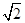 -1.
-1.
练习册系列答案
相关题目
 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,连结椭圆的四个顶点得到的菱形的面积为4.
,连结椭圆的四个顶点得到的菱形的面积为4. ,求直线l的倾斜角.
,求直线l的倾斜角. 的焦距为4,那么
的焦距为4,那么 的值为( )
的值为( )
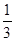


 的左顶点A的斜率为k的直线交椭圆C于另一个点
的左顶点A的斜率为k的直线交椭圆C于另一个点 ,且点
,且点 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点 ,若
,若 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )

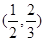

 的焦距为2,则m的取值是 ( )
的焦距为2,则m的取值是 ( )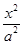 +
+ =1(a>b>0),抛物线C2:x2+by=b2.
=1(a>b>0),抛物线C2:x2+by=b2.
 ,
, b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0, b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程. +
+ =1(a>0,b>0)的右焦点为F(3,0),且点(-3,
=1(a>0,b>0)的右焦点为F(3,0),且点(-3,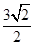 )在椭圆C上,则椭圆C的标准方程为 .
)在椭圆C上,则椭圆C的标准方程为 . +
+ =1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2,若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
=1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2,若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( ) (B)
(B) (C)
(C)  (D)
(D)  -2
-2 =1,过点M(0,1)的直线l交椭圆于A,B两点,O是坐标原点,点P满足
=1,过点M(0,1)的直线l交椭圆于A,B两点,O是坐标原点,点P满足 =
= (
( +
+ ),当l绕点M旋转时,动点P的轨迹方程为 .
),当l绕点M旋转时,动点P的轨迹方程为 .