题目内容
已知椭圆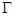 的方程为
的方程为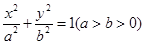 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足 ,求点
,求点 的坐标;
的坐标;
(2)设直线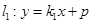 交椭圆
交椭圆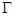 于
于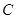 、
、 两点,交直线
两点,交直线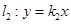 于点
于点 .若
.若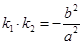 ,证明:
,证明: 为
为 的中点;
的中点;
(3)对于椭圆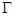 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆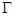 上存在不同的两个交点
上存在不同的两个交点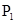 、
、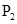 满足
满足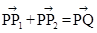 ,写出求作点
,写出求作点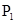 、
、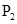 的步骤,并求出使
的步骤,并求出使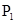 、
、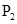 存在的θ的取值范围.
存在的θ的取值范围.
(1)  (2)采用联立方程组结合韦达定理和中点公式来证明。
(2)采用联立方程组结合韦达定理和中点公式来证明。
(3) 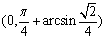
解析试题分析:(1)  ; () 由方程组
; () 由方程组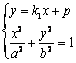 ,消y得方
,消y得方 ,因为直线
,因为直线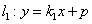 交圆
交圆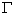 于
于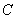 、
、 两点,所以D>0,即
两点,所以D>0,即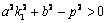 ,设C(x1 ,y1 )、D(x2 ,y2 , D中点坐标为(x0 ,y0 ),则
,设C(x1 ,y1 )、D(x2 ,y2 , D中点坐标为(x0 ,y0 ),则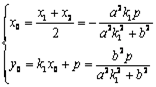 ,由方组
,由方组 ,消y得方(k2 -k1 )xp,又因为
,消y得方(k2 -k1 )xp,又因为 ,所以
,所以 ,故E为CD的中点;
,故E为CD的中点;
(3) 作点P1、P2的步骤:°求出PQ的中点 ,2°求出直线OE的斜率
,2°求出直线OE的斜率 ,3由
,3由 知E为CD的中点,根据()可得CD的斜率
知E为CD的中点,根据()可得CD的斜率 ,4°从而得直线CD的方程:
,4°从而得直线CD的方程: , 5°将直线CD与圆
, 5°将直线CD与圆
Γ的方程联立,方程组的解即为点P1 P2的坐标.
使P1、P2存在,必须点在椭圆内,所以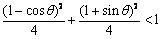 ,化简得
,化简得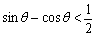 ,
,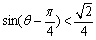 ,又0<q <p,即
,又0<q <p,即 ,所以
,所以 ,故q 的取值范围是
,故q 的取值范围是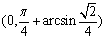 .
.
考点:直线与圆锥曲线的综合
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的前提是要求学生对基础知识有相当熟练的把握。

练习册系列答案
相关题目
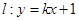 过定点
过定点 ,动点
,动点 满足
满足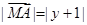 ,动点
,动点 .
.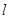 与
与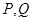 两点,以
两点,以 .
.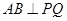 ;②若直线
;②若直线 与
与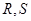 两点,求四边形
两点,求四边形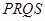 面积的最大值.
面积的最大值.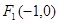 及
及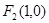 ,点
,点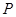 在以
在以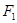 、
、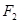 为焦点的椭圆
为焦点的椭圆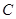 上,且
上,且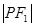 、
、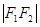 、
、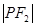 构成等差数列.
构成等差数列.
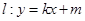 与椭圆
与椭圆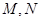 是直线
是直线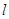 上的两点,且
上的两点,且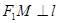 ,
,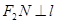 . 求四边形
. 求四边形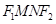 面积
面积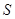 的最大值.
的最大值.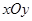 中,
中,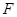 是抛物线
是抛物线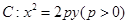 的焦点,
的焦点,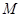 是抛物线
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过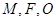 三点的圆的圆心为
三点的圆的圆心为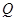 ,点
,点 .
.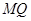 与抛物线
与抛物线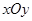 中,以
中,以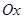 轴为始边作两个锐角
轴为始边作两个锐角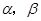 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于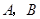 两点.已知
两点.已知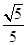 ,
,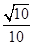 .
.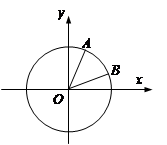
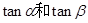 的值;(2)求
的值;(2)求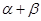 的值.
的值. .
.
 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.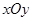 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为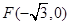 ,右顶点为
,右顶点为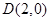 ,设点
,设点 .
.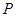 是椭圆上的动点,求线段
是椭圆上的动点,求线段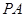 中点
中点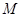 的轨迹方程;
的轨迹方程; 的直线交椭圆于点
的直线交椭圆于点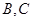 ,求
,求 面积的最大值。
面积的最大值。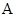 、
、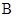 、
、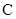 是椭圆
是椭圆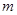 :
: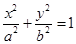 (
(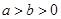 )上的三点,其中点
)上的三点,其中点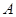 的坐标为
的坐标为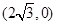 ,
,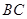 过椭圆的中心,且
过椭圆的中心,且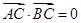 ,
, 。
。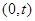 的直线
的直线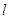 (斜率存在时)与椭圆
(斜率存在时)与椭圆 ,
,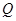 ,设
,设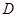 为椭圆
为椭圆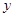 轴负半轴的交点,且
轴负半轴的交点,且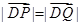 ,求实数
,求实数 的取值范围.
的取值范围.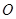 ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为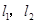 ,经过右焦点
,经过右焦点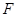 垂直于
垂直于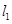 的直线分别交
的直线分别交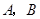 两点.已知
两点.已知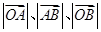 成等差数列,且
成等差数列,且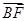 与
与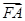 同向.
同向.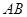 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.