题目内容
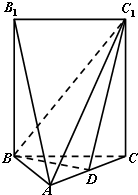 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.(Ⅰ)D在AC上运动,当D在何处时,有AB1∥平面BDC1,并且说明理由;
(Ⅱ)当AB1∥平面BDC1时,求二面角C-BC1-D余弦值.
分析:(I)由题意连接B1C交BC1于O,连接DO由于四边形BCC1B1是矩形且O为B1C中点又D为AC中点,从而DO∥AB1,在由线线平行,利用线面平行的判定定理即可;
(II)由题意建立空间直角坐标系,先求出点B,A,C,D及点C1的坐标,利用先求平面的法向量,在由法向量的夹角与平面的夹角的关系求出二面角的余弦值的大小.
(II)由题意建立空间直角坐标系,先求出点B,A,C,D及点C1的坐标,利用先求平面的法向量,在由法向量的夹角与平面的夹角的关系求出二面角的余弦值的大小.
解答: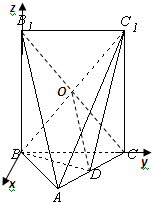 解:(Ⅰ)当D为AC中点时,有AB1∥平面BDC1,
解:(Ⅰ)当D为AC中点时,有AB1∥平面BDC1,
证明:连接B1C交BC1于O,连接DO∵四边形BCC1B1是矩形
∴O为B1C中点又D为AC中点,从而DO∥AB,
∵AB1?平面BDC1,DO?平面BDC1∴AB1∥平面BDC1
(Ⅱ)建立空间直角坐标系B-xyz如图所示,则B(0,0,0),A(
,1,0),C(0,2,0),D(
,
,0),C1(0,2,2
),
所以
=(
,
,0),
=(0,2,2
).
设
=(x,y,z)为平面BDC1的法向量,则有
,即
令Z=1,可得平面BDC1的一个法向量为
=(3,-
,1),
而平面BCC1的一个法向量为
=(1,0,0),
所以cos<
,
>=
=
=
,故二面角C-BC1-D的余弦值为
.
 解:(Ⅰ)当D为AC中点时,有AB1∥平面BDC1,
解:(Ⅰ)当D为AC中点时,有AB1∥平面BDC1,证明:连接B1C交BC1于O,连接DO∵四边形BCC1B1是矩形
∴O为B1C中点又D为AC中点,从而DO∥AB,
∵AB1?平面BDC1,DO?平面BDC1∴AB1∥平面BDC1
(Ⅱ)建立空间直角坐标系B-xyz如图所示,则B(0,0,0),A(
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
所以
| BD |
| ||
| 2 |
| 3 |
| 2 |
| BC1 |
| 3 |
设
| n1 |
|
|
令Z=1,可得平面BDC1的一个法向量为
| n1 |
| 3 |
而平面BCC1的一个法向量为
| n2 |
所以cos<
| n1 |
| n2 |
| ||||
|
|
| 3 | ||
|
3
| ||
| 13 |
3
| ||
| 13 |
点评:(I)此问重点考查了线面平行的判定定理,还考查了中位线的平行的性质定理,及学生的空间想象能力
(II)此问重点考查了利用空间向量的知识,及平面的法向量的夹角与二面角的大小联系;此外还考查了学生的计算能力.
(II)此问重点考查了利用空间向量的知识,及平面的法向量的夹角与二面角的大小联系;此外还考查了学生的计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
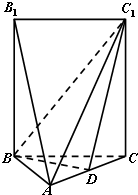 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角. 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.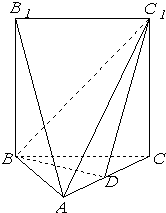 如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.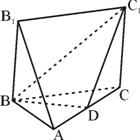 (1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;
(1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;