题目内容
给定下列命题:
①函数y=sin(
-2x)的单增区间是[kπ-
,kπ+
](k∈Z);
②已知|
|=|
|=2,
与
的夹角为
,则
+
在
上的投影为3;
③函数y=f(x)与y=f-1(x)-1的图象关于直线x-y+1=0对称;
④已知f(x)=asinx-bcosx,(a,b∈R)在x=
处取得最小值,则f(
-x)=-f(x);
⑤若sinx+siny=
,则siny-cos2x的最大值为
.
则真命题的序号是
①函数y=sin(
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
②已知|
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| a |
③函数y=f(x)与y=f-1(x)-1的图象关于直线x-y+1=0对称;
④已知f(x)=asinx-bcosx,(a,b∈R)在x=
| π |
| 4 |
| 3π |
| 2 |
⑤若sinx+siny=
| 1 |
| 3 |
| 4 |
| 3 |
则真命题的序号是
①②③④
①②③④
.分析:①函数y=sin(
-2x)的增区间满足-
+2kπ≤
-2x≤
+2kπ,k∈Z,故①正确;
②
+
在
上的投影为2+2xsin30°=3,故②正确;
③由函数y=f(x)与y=f-1(x)图象关于直线x-y=0对称,知③正确;
④由f(x)=asinx-bcosx=
sin(x-θ)在x=
处取得最小值,其中tanθ=
,得θ=-
,所以f(
-x)=-f(x),故④成立;
⑤sinx+siny=
,siny=
-sinx,由此能导出sinx=-
时,有ωmax=-
,故⑤不正确.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
②
| a |
| b |
| a |
③由函数y=f(x)与y=f-1(x)图象关于直线x-y=0对称,知③正确;
④由f(x)=asinx-bcosx=
| a2+b2 |
| π |
| 4 |
| b |
| a |
| 5π |
| 4 |
| 3π |
| 2 |
⑤sinx+siny=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 13 |
| 24 |
解答:解:①函数y=sin(
-2x)的增区间满足-
+2kπ≤
-2x≤
+2kπ,k∈Z,
∴函数y=sin(
-2x)的增区间是[kπ-
,kπ+
](k∈Z),故①正确;
②∵|
|=|
|=2,
与
的夹角为
,
∴
+
在
上的投影为|
|+|
|•sin(
)=2+2xsin30°=2+1=3,故②正确;
③由函数y=f(x)与y=f-1(x)图象关于直线x-y=0对称,
知函数y=f(x)与y=f-1(x)-1的图象关于直线x-y+1=0对称,故③正确;
④∵f(x)=asinx-bcosx=
sin(x-θ)在x=
处取得最小值,其中tanθ=
,
所以
-θ=
,得θ=-
,
所以f(
-x)=-f(x),故④成立;
⑤sinx+siny=
,siny=
-sinx,
由-1≤siny≤1,-1≤sinx≤1得
-1≤
-sinx≤1
-
≤sinx≤1
ω=siny-cos2x
=
-sinx-2sin2x-1
=-2sin2x-sinx-
=-2(sinx+
)2-
sinx=-
时,有ωmax=-
,故⑤不正确.
故答案为:①②③④.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴函数y=sin(
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
②∵|
| a |
| b |
| a |
| b |
| π |
| 3 |
∴
| a |
| b |
| a |
| a |
| b |
| ||
| 2 |
③由函数y=f(x)与y=f-1(x)图象关于直线x-y=0对称,
知函数y=f(x)与y=f-1(x)-1的图象关于直线x-y+1=0对称,故③正确;
④∵f(x)=asinx-bcosx=
| a2+b2 |
| π |
| 4 |
| b |
| a |
所以
| π |
| 4 |
| 3π |
| 2 |
| 5π |
| 4 |
所以f(
| 3π |
| 2 |
⑤sinx+siny=
| 1 |
| 3 |
| 1 |
| 3 |
由-1≤siny≤1,-1≤sinx≤1得
-1≤
| 1 |
| 3 |
-
| 2 |
| 3 |
ω=siny-cos2x
=
| 1 |
| 3 |
=-2sin2x-sinx-
| 2 |
| 3 |
=-2(sinx+
| 1 |
| 4 |
| 13 |
| 24 |
sinx=-
| 1 |
| 4 |
| 13 |
| 24 |
故答案为:①②③④.
点评:本题考查命题的真假判断,解题时要认真审题,仔细解答,注意三角函数、向量、函数对称性等知识点的应用,解题时要认真审题,仔细解答.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
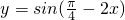 的单增区间是
的单增区间是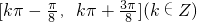 ;
; 的夹角为
的夹角为 ,则
,则 在
在 上的投影为3;
上的投影为3; 处取得最小值,则
处取得最小值,则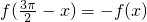 ;
;