题目内容
给定下列命题:
①函数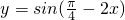 的单增区间是
的单增区间是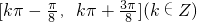 ;
;
②已知 的夹角为
的夹角为 ,则
,则 在
在 上的投影为3;
上的投影为3;
③函数y=f(x+1)与y=f-1(x)-1的图象关于直线x-y=0对称;
④已知f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则
处取得最小值,则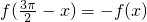 ;
;
则真命题的序号是________.
②③④
分析:①根据诱导公式进行化简,再由正弦函数的单调性可求其单调增区间,进而判断①为假命题;
②利用向量投影的概念,计算可得结论;
③判断函数y=f(x+1)与y=f-1(x)-1互为反函数即可;
④已知f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则函数关于直线
处取得最小值,则函数关于直线 对称,不妨设函数解析式为f(x)=
对称,不妨设函数解析式为f(x)= ,即可得到结论.
,即可得到结论.
解答:①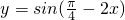 =
= ,由
,由 ,可得
,可得 为函数的单调递增区间,故①为假命题;
为函数的单调递增区间,故①为假命题;
② 在
在 上的投影为
上的投影为 =
= ,故②正确;
,故②正确;
③由函数y=f(x+1)可得x=f-1(y)-1,再将x,y互换可得y=f-1(x)-1,故函数y=f(x+1)与y=f-1(x)-1的图象关于直线x-y=0对称,即③正确;
④已知f(x)=asinx-bcosx,(a,b∈R)在 处取得最小值,则函数关于直线
处取得最小值,则函数关于直线 对称,不妨设函数解析式为f(x)=
对称,不妨设函数解析式为f(x)= ,
,
∴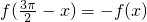 ,即④正确.
,即④正确.
故真命题的序号为:②③④
点评:本题考查命题真假的判断,考查函数的单调性,考查向量知识,考查三角函数的性质,综合性强.
分析:①根据诱导公式进行化简,再由正弦函数的单调性可求其单调增区间,进而判断①为假命题;
②利用向量投影的概念,计算可得结论;
③判断函数y=f(x+1)与y=f-1(x)-1互为反函数即可;
④已知f(x)=asinx-bcosx,(a,b∈R)在
 处取得最小值,则函数关于直线
处取得最小值,则函数关于直线 对称,不妨设函数解析式为f(x)=
对称,不妨设函数解析式为f(x)= ,即可得到结论.
,即可得到结论.解答:①
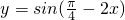 =
= ,由
,由 ,可得
,可得 为函数的单调递增区间,故①为假命题;
为函数的单调递增区间,故①为假命题;②
 在
在 上的投影为
上的投影为 =
= ,故②正确;
,故②正确;③由函数y=f(x+1)可得x=f-1(y)-1,再将x,y互换可得y=f-1(x)-1,故函数y=f(x+1)与y=f-1(x)-1的图象关于直线x-y=0对称,即③正确;
④已知f(x)=asinx-bcosx,(a,b∈R)在
 处取得最小值,则函数关于直线
处取得最小值,则函数关于直线 对称,不妨设函数解析式为f(x)=
对称,不妨设函数解析式为f(x)= ,
,∴
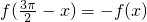 ,即④正确.
,即④正确.故真命题的序号为:②③④
点评:本题考查命题真假的判断,考查函数的单调性,考查向量知识,考查三角函数的性质,综合性强.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目