题目内容
已知椭圆具有性质:若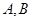 是椭圆
是椭圆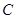 :
: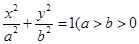 且
且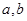 为常数
为常数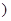 上关于原点对称的两点,点
上关于原点对称的两点,点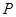 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线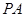 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为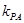 ,
,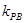 ,那么
,那么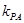 与
与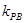 之积是与点
之积是与点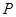 位置无关的定值
位置无关的定值 .
.
试对双曲线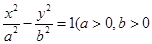 且
且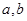 为常数
为常数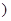 写出类似的性质,并加以证明.
写出类似的性质,并加以证明.
双曲线类似的性质为:若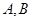 是双曲线
是双曲线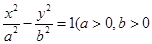 且
且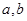 为常数
为常数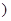 上关于原点对称的两点,点
上关于原点对称的两点,点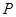 是双曲线上的任意一点,若直线
是双曲线上的任意一点,若直线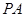 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为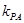 ,
,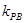 ,那么
,那么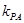 与
与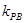 之积是与点
之积是与点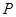 位置无关的定值
位置无关的定值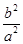 .
.
解析试题分析:双曲线类似的性质为:若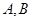 是双曲线
是双曲线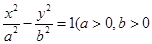 且
且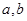 为常数
为常数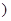 上关于原点对称的两点,点
上关于原点对称的两点,点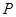 是双曲线上的任意一点,若直线
是双曲线上的任意一点,若直线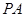 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为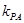 ,
,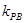 ,那么
,那么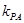 与
与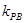 之积是与点
之积是与点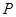 位置无关的定值
位置无关的定值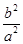 .
.
证明:设 ,
, ,则
,则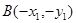 ,
,
且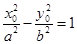 ①,
①,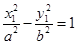 ②,
②,
两式相减得: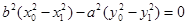 ,
,
所以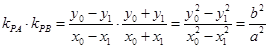 是与点
是与点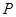 位置无关的定值.
位置无关的定值.
考点:本题主要考查双曲线的几何性质,直线与双曲线、椭圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题主要运用双曲线的几何性质。(2)作为研究直线的斜率乘积是否为定值问题,应用韦达定理,通过“整体代换”,简化了探究过程。

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率为
轴上,离心率为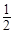 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线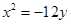 的焦点.
的焦点.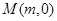 的直线
的直线 与椭圆
与椭圆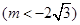 ,直线
,直线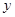 轴交于点
轴交于点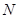 ,当
,当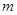 为何值时
为何值时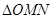 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.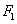 和
和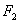 ,且|
,且|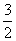 )在该椭圆上.
)在该椭圆上.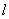 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A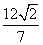 ,求以
,求以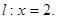 动圆M与定圆
动圆M与定圆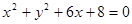 外切且与直线
外切且与直线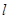 相切.
相切.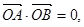 求证直线AB过一定点,并求出定点的坐标.
求证直线AB过一定点,并求出定点的坐标.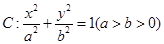 的左右焦点分别为
的左右焦点分别为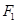 、
、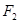 ,离心率
,离心率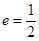 ,直线
,直线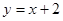 经过左焦点
经过左焦点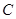 的方程;
的方程;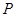 为椭圆
为椭圆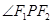 的范围.
的范围.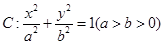 的离心率为
的离心率为 ,两焦点分别为
,两焦点分别为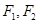 ,点
,点 是椭圆C上一点,
是椭圆C上一点, 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为 .
.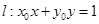 与圆O的位置关系.
与圆O的位置关系.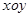 中,直线
中,直线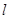 的参数方程为
的参数方程为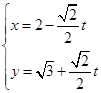 (t 为参数)。在极坐标系(与直角坐标系
(t 为参数)。在极坐标系(与直角坐标系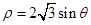 。
。 ),求|PA|+|PB|.
),求|PA|+|PB|. =2x于M(x
=2x于M(x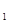 ,y
,y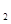 ,y
,y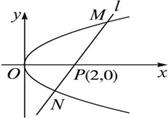
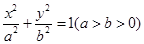 的两个焦点为F1、F2,点B1为其短轴的一个端点,满足
的两个焦点为F1、F2,点B1为其短轴的一个端点,满足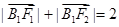 ,
,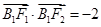 。
。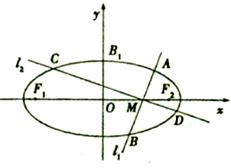
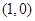 做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。