题目内容
若(1-2x)2012=a0+a1x+a2x2+…+a2011x2011+a2012x2012(x∈R),则(a0+a1)+(a0+a2)+(a0+a3)+…+(a0+a2010)+(a0+a2011) +(a0+a2012)=( )
| A.2009 | B.2010 | C.2011 | D.2012 |
D
令x=1,则 ,
,
所以(a0+a1)+(a0+a2)+(a0+a3)+…+(a0+a2010)+(a0+a2011) +(a0+a2012)
=2012a0+ =2012.
=2012.
 ,
,所以(a0+a1)+(a0+a2)+(a0+a3)+…+(a0+a2010)+(a0+a2011) +(a0+a2012)
=2012a0+
 =2012.
=2012.
练习册系列答案
相关题目
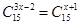 ,求x的值。
,求x的值。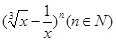 的展开式中第3项为常数项,求
的展开式中第3项为常数项,求 .
. 其中
其中 是常数,计算
是常数,计算 =______________.
=______________.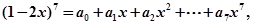 那么
那么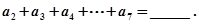
 ,
,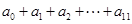 的值为( )
的值为( )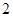



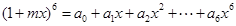 ,且
,且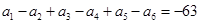 ,则实数m的值为
,则实数m的值为  的展开式中,
的展开式中,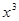 的系数是
的系数是 