Question

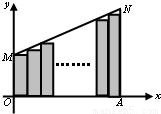
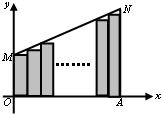线段C：y=x+2（0≤x≤2）两端分别为M、N，且NA⊥x轴于点A．把线段OA分成n等份，以每一段为边作矩形，使与x轴平行的边一个端点在C上，另一端点在C的下方（如图），设这n个矩形的面积之和为S_n，则S_n=

 

．

Answer 1

分析：根据题意可知从原点出发，矩形的长成等差数列，首项为2，公差为

2

n

，进而根据矩形面积公式，通过等差数列的求和公式求得答案．

解答：解：依题意可知从原点出发，矩形的长成等差数列，首项为2，公差为

2

n

，则
S_n=

2

n

[2+（

2

n

+2）+（

4

n

+2）+…+

2n-2

n

+2）]=

1

n

•

[2+ 2n-2 n +2]n

2

=6-

2

n

．
故答案为6-

2

n

．

点评：本题主要考查了等差数列的求和，属基础题．