题目内容
已知函数fn(x)＝(1＋x)n－1，(n∈N*，且n＞1)．
(Ⅰ)设函数h(x)＝f3(x)－F2(x)，x∈[－2，0]，求h(x)的最大值和最小值
(Ⅱ)若x＞－2求证：fn(x)≥nx．
答案：
解析：
解析：
|
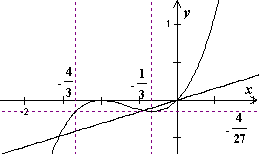
(Ⅰ)h(x)＝f3(x)－f2(x)＝x(1＋x)2， ∴ 令
∴h(x)在(－2，－1)，(－
(Ⅱ)令g(x)＝fn(x)－nx＝(1＋x)n－1－nx． 则 ∴当－2＜x＜0时， ∴g(x)在(－2，0)上单调递减，在(0，＋∞)上单调递增． ∴当x＝0时，g(x)min＝g(0)＝0，即g(0)≥g(x)min＝0，∴fn(x)≥nx．13分 |
(x)＝(1＋x)2＋2x(1＋x)＝(1＋x)(1＋3x)，
，8分
，0)上单调递增，在(－1，－
)上单调递减，过点(0，0)．
时，
7分
(x)＝n(x＋1)n－1－n＝n[(x＋1)n－1－1]，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，fn+1(x)＝f1[fn(x)](n＝1，2，3，…)，f2 002(x)是
(n∈N*)．
(0)与
的大小；
．
，求
的最大值和最小值
求证：fn(x)≥nx.