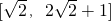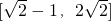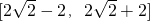题目内容
设集合
，
，且A∩B≠∅，则实数a的取值范围是（ ）A．[-2，2]
B．
C．
D．
【答案】分析：由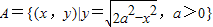
，我们易得A集合表示以原点为圆心，以
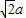为半径的圆在X轴上方的部分，
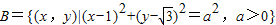，B集合表示以（1，
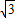）为原点以a为半径的圆，根据A∩B≠∅，我们对a进行分析讨论，我们易得到结论．
解答：解：∵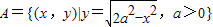
∴A集合表示以原点为圆心，
以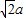
为半径的圆在X轴上方的部分，
又∵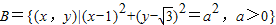
，
∴B集合表示以（1，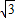
）为原点以a为半径的圆
若A∩B≠∅，则两个圆相切或相交
故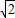
a-a≤2≤
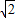a+a
解得a∈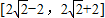
故选D．
点评：本题考查的知识点是两个集合的交集运算及圆与圆之间的位置关系，根据A∩B≠∅，准确判断两个圆的位置关系，并根据圆的位置关系列出两圆半径与圆心距的关系，是解答的关键．
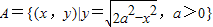，我们易得A集合表示以原点为圆心，以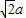为半径的圆在X轴上方的部分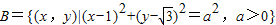，，B集合表示以（1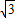，）为原点以a为半径的圆，根据A∩B≠∅，我们对a进行分析讨论，我们易得到结论．解答：解：∵
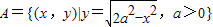
∴A集合表示以原点为圆心，
以
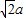为半径的圆在X轴上方的部分，又∵
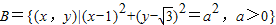，∴B集合表示以（1，
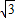）为原点以a为半径的圆若A∩B≠∅，则两个圆相切或相交
故
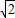a-a≤2≤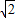a+a解得a∈
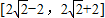
故选D．
点评：本题考查的知识点是两个集合的交集运算及圆与圆之间的位置关系，根据A∩B≠∅，准确判断两个圆的位置关系，并根据圆的位置关系列出两圆半径与圆心距的关系，是解答的关键．
练习册系列答案
相关题目
，
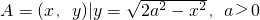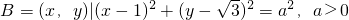，且A∩B≠∅，则实数a的取值范围是
