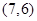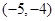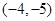题目内容
设动点P在直线x=1上,O为坐标原点,以OP为直角边、点O为直角顶点作等腰直角△OPQ,则动点Q的轨迹是( )
| A.圆 | B.两条平行直线 |
| C.抛物线 | D.双曲线 |
B
解析

练习册系列答案
相关题目
已知点 ,
, ,
, ,若线段
,若线段 和
和 有相同的垂直平分线,则点
有相同的垂直平分线,则点 的坐标是( )
的坐标是( )
A. | B. |
C. | D. |
直线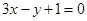 的斜率是( )
的斜率是( )
A.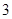 | B.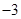 | C.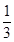 | D.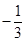 |
已知圆 ,点
,点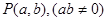 是圆
是圆 内的一点,过点
内的一点,过点 的圆
的圆 的最短弦在直线
的最短弦在直线 上,直线
上,直线 的方程为
的方程为 ,那么( )
,那么( )
A. 且 且 与圆 与圆 相交 相交 | B. 且 且 与圆 与圆 相切 相切 |
C. 且 且 与圆 与圆 相离 相离 | D. 且 且 与圆 与圆 相离 相离 |
已知三条直线a,b,c,若a和b是异面直线,b和c是异面直线,那么直线a和c的位置关系是( )
| A.平行 | B.相交 | C.异面 | D.平行、相交或异面 |
点A(1,1)到直线xcosθ+ysinθ-2=0的距离的最大值是( )
| A.2 | B.2-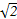 |
C.2+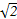 | D.4 |
已知△ABC三顶点坐标A(1,2),B(3,6),C(5,2),M为AB中点,N为AC中点,则直线MN的方程为( )
| A.2x+y-8=0 | B.2x-y+8=0 |
| C.2x+y-12=0 | D.2x-y-12=0 |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,半径为的圆的方程为( )
| A.x2+y2-2x+4y=0 |
| B.x2+y2+2x+4y=0 |
| C.x2+y2+2x-4y=0 |
| D.x2+y2-2x-4y=0 |
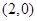 与点
与点 重合,则与点
重合,则与点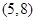 重合的点是( )
重合的点是( )