题目内容
已知ω>0,a=(2sinωx+cosωx,2sinωx-cosωx),b=(sinωx,cosωx).f(x)=a·b.f(x)图象上相邻的两个对称轴的距离是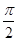 .
.
(1)求ω的值;
(2)求函数f(x)在区间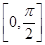 上的最大值和最小值.
上的最大值和最小值.
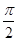 .
.(1)求ω的值;
(2)求函数f(x)在区间
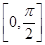 上的最大值和最小值.
上的最大值和最小值.(1)1(2)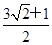
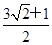
f(x)=a·b
=(2sinωx+cosωx)sinωx+(2sinωx-cosωx)cosωx=2sin2ωx+3sinωxcosωx-cos2ωx
=1-cos2ωx+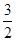 sin2ωx-
sin2ωx-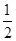 (1+cos2ωx)
(1+cos2ωx)
=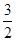 (sin2ωx-cos2ωx)+
(sin2ωx-cos2ωx)+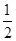 =
=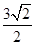 sin
sin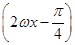 +
+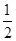 .
.
(1)因为函数f(x)的图象上相邻的两个对称轴间的距离是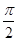 ,所以函数f(x)的最小正周期T=π,则ω=1.
,所以函数f(x)的最小正周期T=π,则ω=1.
(2)ω=1,f(x)=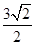 sin
sin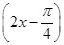 +
+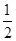 .
.
∴x∈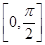 ,∴2x-
,∴2x-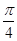 ∈
∈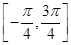 ,
,
则当2x-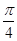 =-
=-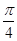 ,即x=0时,f(x)取得最小值-1;
,即x=0时,f(x)取得最小值-1;
当2x-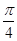 =
=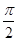 ,即x=
,即x=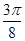 时,f(x)取得最大值
时,f(x)取得最大值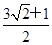
=(2sinωx+cosωx)sinωx+(2sinωx-cosωx)cosωx=2sin2ωx+3sinωxcosωx-cos2ωx
=1-cos2ωx+
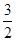 sin2ωx-
sin2ωx-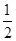 (1+cos2ωx)
(1+cos2ωx)=
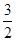 (sin2ωx-cos2ωx)+
(sin2ωx-cos2ωx)+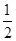 =
=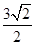 sin
sin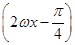 +
+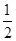 .
.(1)因为函数f(x)的图象上相邻的两个对称轴间的距离是
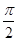 ,所以函数f(x)的最小正周期T=π,则ω=1.
,所以函数f(x)的最小正周期T=π,则ω=1.(2)ω=1,f(x)=
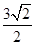 sin
sin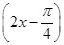 +
+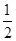 .
.∴x∈
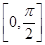 ,∴2x-
,∴2x-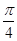 ∈
∈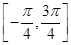 ,
,则当2x-
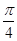 =-
=-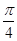 ,即x=0时,f(x)取得最小值-1;
,即x=0时,f(x)取得最小值-1;当2x-
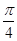 =
=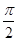 ,即x=
,即x=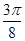 时,f(x)取得最大值
时,f(x)取得最大值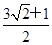

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
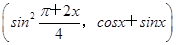 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.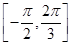 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;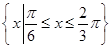 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A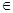 B,求实数m的取值范围.
B,求实数m的取值范围.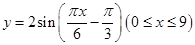 的最大值与最小值之差为( )
的最大值与最小值之差为( )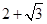



 π
π π
π -
- )(0≤x≤9)的最大值与最小值之和为( )
)(0≤x≤9)的最大值与最小值之和为( )
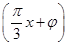 ,x∈R,A>0,0<φ<
,x∈R,A>0,0<φ<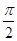 ,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).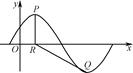
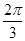 ,求A的值.
,求A的值. sinωxsin
sinωxsin (ω>0)的最小正周期为
(ω>0)的最小正周期为 .
. 上的取值范围.
上的取值范围. 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是____________________.
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是____________________.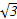 sinxcosx-1(x∈R).
sinxcosx-1(x∈R).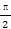 ],求函数f(x)的最大值与最小值.
],求函数f(x)的最大值与最小值.