题目内容
(本题满分12分)
已知等差数列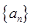 满足:
满足: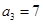 ,
, ,
,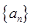 的前n项和为
的前n项和为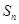 .
.
(Ⅰ) 求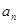 及
及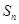 ;
;
(Ⅱ) 令 (
( ),求数列
),求数列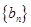 的前n项和
的前n项和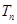 .
.
(1)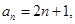
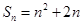 ((2)
((2)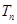 =
=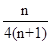
解析试题分析:(Ⅰ)设等差数列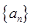 的公差为
的公差为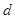 ,因为
,因为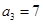 ,
, ,
,
所以有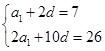 ,解得
,解得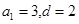 , ……2分
, ……2分
所以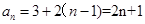 ; ……4分
; ……4分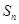 =
=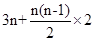 =
= . ……6分
. ……6分
(Ⅱ)由(Ⅰ)知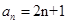 ,
,
所以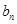 =
=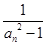 =
=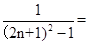
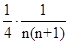 =
=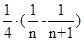 , ……8分
, ……8分
所以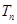 =
=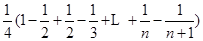 =
=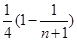 =
=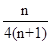 ,
,
即数列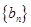 的前n项和
的前n项和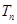 =
=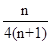 . ……12分
. ……12分
考点:本小题主要考查等差数列的通项公式、等差数列的前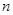 项和公式的应用和裂项相消法求数列的前
项和公式的应用和裂项相消法求数列的前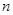 项和,考查了学生的运算求解能力.
项和,考查了学生的运算求解能力.
点评:使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
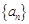 中,
中,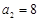 ,前10项的和
,前10项的和
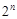 ,…项,按原来的顺序排成一个新的数列
,…项,按原来的顺序排成一个新的数列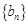 ,试求新数列
,试求新数列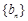 的前
的前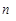 项和
项和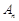 .
.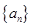 的前
的前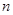 项和为
项和为 ,若
,若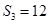 ,且
,且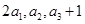 成等比数列.求
成等比数列.求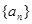 中,
中,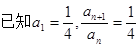 ,
, .求
.求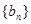 的通项公式.
的通项公式. 的前
的前 项和为
项和为 ,且满足
,且满足 为常数,则称该数列为
为常数,则称该数列为 数列.
数列. 是否为
是否为 且公差不为零的等差数列
且公差不为零的等差数列 满足
满足 ,求
,求 的最小值
的最小值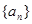 中,
中,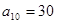 ,
, .
.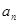 ;
;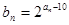 ,证明:数列
,证明:数列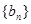 为等比数列;
为等比数列; 的前
的前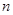 项和
项和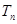 .
. 的前
的前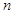 项和为
项和为 ,且
,且 ,数列
,数列 中,
中, ,点
,点 在直线
在直线 上.
上. 的通项
的通项 和
和 ;
; ,求数列
,求数列 的前n项和
的前n项和 ,并求满足
,并求满足 的最大正整数
的最大正整数 ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn}, 的前n项和为
的前n项和为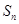 ,点
,点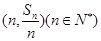 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.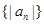 的前n项的和.
的前n项的和.