Question

【题目】函数f（x）=lnx﹣ax2+x有两个零点，则实数a的取值范围是（ ）
A.（0，1）
B.（﹣∞，1）
C.（﹣∞， ）
D.（0， ）

Answer 1

【答案】A
【解析】解：∵函数f（x）=lnx﹣ax2+x有两个不同的零点， 不妨令g（x）=lnx，h（x）=ax2﹣x，
将零点问题转化为两个函数交点的问题；
又函数h（x）=x（ax﹣1），
当a≤0时，g（x）和h（x）只有一个交点，不满足题意；
当a＞0时，由lnx﹣ax2+x=0，得a= ；
令r（x）= ，则r′（x）= = ，
当0＜x＜1时，r'（x）＞0，r（x）是单调增函数，
当x＞1时，r'（x）＜0，r（x）是单调减函数，且 ＞0，∴0＜a＜1；
或当a＞0时，作出两函数g（x）=lnx，h（x）=ax2﹣x的图象，如图所示；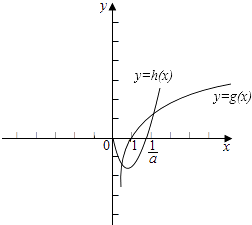
g（x）=lnx交x轴于点（1，0），
h（x）=ax2﹣x交x轴于点（0，0）和点（ ，0）；
要使方程有两个零点，应满足两函数有两个交点，
即 ＞1，解得0＜a＜1；
∴a的取值范围是（0，1）．
故选：A．
函数f（x）=lnx﹣ax2+x有两个不同的零点，转化为函数g（x）=lnx和h（x）=ax2﹣x交点的问题；
讨论a≤0时不满足题意，a＞0时，求得（a）max=1，当x→+∞时，a→0，从而可得答案．
或a＞0时，作出两函数g（x）=lnx，h（x）=ax2﹣x的图象，由 ＞1求出a的取值范围．