题目内容

在Rt△OAB中，∠O=90°，则 cos2A+cos2B=1．根据类比推理的方法，在三棱锥O﹣ABC中，OA⊥OB，OB⊥OC，OC⊥OA，α、β、γ 分别是三个侧面与底面所成的二面角，则　

．

考点：

类比推理；二面角的平面角及求法．

专题：

空间角．

分析：

确定三个侧面两两互相垂直，利用类比的方法，即可得到结论．

解答：

解：在Rt△OAB中，cos2A+cos2B===1．

∵OA⊥OB，OB⊥OC，OC⊥OA，∴三个侧面两两互相垂直，

于是类比到三棱锥O﹣ABC中，猜想三棱锥O﹣ABC中，若三个侧面分别与底面所成的角为α、β、γ，则cos2α+cos2β+cos2γ=1．故答案为cos2α+cos2β+cos2γ=1．

点评：

本题考查类比推理，考查学生分析解决问题的能力，属于中档题．

　

练习册系列答案
相关题目
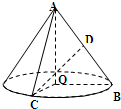精英家教网如图，在Rt△AOB中，∠OAB=
π6
，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B-AO-C是直二面角．动点D在斜边AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当D为AB的中点时，求异面直线AO与CD所成角的余弦值大小；
（Ⅲ）求CD与平面AOB所成角最大时的正切值大小．
在Rt△OAB中，∠O=90°，则 cos2A+cos2B=1．根据类比推理的方法，在三棱锥O-ABC中，OA⊥OB，OB⊥OC，OC⊥OA，α、β、γ 分别是三个侧面与底面所成的二面角，则
cos2α+cos2β+cos2γ=1
cos2α+cos2β+cos2γ=1
．
精英家教网如图，在 Rt△AOB中，∠OAB=
π6
，斜边AB=4，D是AB的中点．现将 Rt△AOB以直角边AO为轴旋转一周得到一个圆锥体，点C为圆锥体底面圆周上的一点，且∠BOC=90°．
（1）求异面直线AO与CD所成角的大小；
（2）若某动点在圆锥体侧面上运动，试求该动点从点C出发运动到点D所经过的最短距离．
在Rt△OAB中，∠O=90°，则 cos2A+cos2B=1．根据类比推理的方法，在三棱锥O-ABC中，OA⊥OB，OB⊥OC，OC⊥OA，α、β、γ 分别是三个侧面与底面所成的二面角，则    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网