题目内容
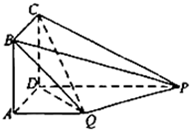 如图,四边形ABCD为长方形,PD⊥平面ABCD,PD∥QA,QA=AD=
如图,四边形ABCD为长方形,PD⊥平面ABCD,PD∥QA,QA=AD=| 1 |
| 2 |
(Ⅰ)证明:平面PQC⊥平面DCQ;
(Ⅱ)若二面角Q-BP-C的大小等于
| 3π |
| 4 |
| AB |
| AD |
分析:(Ⅰ)建立空间坐标系,用坐标表示点与向量,证明
•
=0,
•
=0即可证得结论;
(Ⅱ)求出平面PBC的法向量
=(0,t,2),平面PBQ的法向量
=(t,t,1),利用向量的夹角公式,即可求得结论.
| PQ |
| DQ |
| PQ |
| DC |
(Ⅱ)求出平面PBC的法向量
| n |
| m |
解答: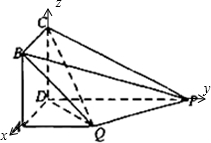 (Ⅰ)证明:设DA=1,AB=t,建立如图空间坐标系D-xyz,则Q(1,1,0),C(0,0,t),P(0,2,0)
(Ⅰ)证明:设DA=1,AB=t,建立如图空间坐标系D-xyz,则Q(1,1,0),C(0,0,t),P(0,2,0)
∴
=(1,1,0),
=(0,0,t),
=(1,-1,0)
∴
•
=0,
•
=0
∴PQ⊥DQ,PQ⊥DC
∵DC∩DQ=D,∴PQ⊥平面DCQ
∴平面PQC⊥平面DCQ;
(Ⅱ)解:
=(1,0,0),
=(-1,2,-t)
设
=(x,y,z)是平面PBC的法向量,则
,即
,取
=(0,t,2)
设
=(x′,y′,z′)是平面PBQ的法向量,则
,即
,取
=(t,t,1)
∴|cos<
,
>|=|
|=
=
,∴t=2
∴二面角Q-BP-C的大小等于
时,
=2.
 (Ⅰ)证明:设DA=1,AB=t,建立如图空间坐标系D-xyz,则Q(1,1,0),C(0,0,t),P(0,2,0)
(Ⅰ)证明:设DA=1,AB=t,建立如图空间坐标系D-xyz,则Q(1,1,0),C(0,0,t),P(0,2,0)∴
| DQ |
| DC |
| PQ |
∴
| PQ |
| DQ |
| PQ |
| DC |
∴PQ⊥DQ,PQ⊥DC
∵DC∩DQ=D,∴PQ⊥平面DCQ
∴平面PQC⊥平面DCQ;
(Ⅱ)解:
| CB |
| BP |
设
| n |
|
|
| n |
设
| m |
|
|
| m |
∴|cos<
| m |
| n |
| ||||
|
|
| t2+2 | ||||
|
| ||
| 2 |
∴二面角Q-BP-C的大小等于
| 3π |
| 4 |
| AB |
| AD |
点评:本题考查面面垂直,考查面面角,考查利用向量知识解决立体几何问题,关键是建立空间直角坐标系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=