题目内容
把函数f(x)=2sin(2x+φ)(0<φ<π)的图象向左平移
个单位后得到偶函数g(x)的图象.
(Ⅰ)求φ的值;
(Ⅱ)求函数h(x)=f(x-
)-g(x)的单调增区间.
| π |
| 6 |
(Ⅰ)求φ的值;
(Ⅱ)求函数h(x)=f(x-
| π |
| 12 |
(I)把函数f(x)=2sin(2x+φ)(0<φ<π)的图象向左平移
个单位后得到:
g(x)=2sin[2(x+
)+φ]的图象,
∵函数g(x)为偶函数,
故当x=0时,2×
+φ=
+kπ,即φ=
+kπ,k∈Z,
又∵0<φ<π,
∴φ=
,
(II)由(I)得:f(x)=2sin(2x+
),
∴f(x-
)=2sin2x
g(x)=2sin(2x+
)=2cos2x,
∴h(x)=f(x-
)-g(x)=2sin2x-2cos2x=2
sin(2x+
),
由2x+
∈[-
+2kπ,
+2kπ]得:x∈[-
+2kπ,
+2kπ],(k∈Z),
故函数h(x)=f(x-
)-g(x)的单调增区间为[-
+2kπ,
+2kπ],(k∈Z)
| π |
| 6 |
g(x)=2sin[2(x+
| π |
| 6 |
∵函数g(x)为偶函数,
故当x=0时,2×
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
又∵0<φ<π,
∴φ=
| π |
| 6 |
(II)由(I)得:f(x)=2sin(2x+
| π |
| 6 |
∴f(x-
| π |
| 12 |
g(x)=2sin(2x+
| π |
| 2 |
∴h(x)=f(x-
| π |
| 12 |
| 2 |
| π |
| 4 |
由2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
故函数h(x)=f(x-
| π |
| 12 |
| 3π |
| 8 |
| π |
| 8 |

练习册系列答案
相关题目



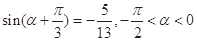 则
则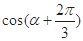 等于( ).
等于( ).



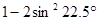 的结果等于______.
的结果等于______.