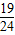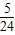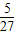题目内容
已知点A在坐标原点,点B在直线y=1上,点C(3,4),若AB≤
,则△ABC的面积大于5的概率是( )
| 10 |
分析:先求出满足△ABC的面积大于5的点B的轨迹长度及满足|AB|≤
的点B的轨迹长度,再利用几何概率的计算公式即可得出.
| 10 |
解答:解:如图所示,设B(x,1),
∵|AB|≤
,∴
≤
,化为x2≤9,解得-3≤x≤3.
设点B到直线AB的距离为h,∵|AC|=5,S△ABC=
|AC|h>5,∴h>2.
又直线AB的方程为y=
x,即4x-3y=0,∴h=
.
解
>2,-3≤x≤3得-3≤x<-
,其长度=
.
∴△ABC的面积大于5的概率P=
=
.
故选C.
∵|AB|≤
| 10 |
| x2+1 |
| 10 |
设点B到直线AB的距离为h,∵|AC|=5,S△ABC=
| 1 |
| 2 |
又直线AB的方程为y=
| 4 |
| 3 |
| |4x-3| | ||
|
解
| |4x-3| |
| 5 |
| 7 |
| 4 |
| 5 |
| 4 |
∴△ABC的面积大于5的概率P=
| ||
| 6 |
| 5 |
| 24 |
故选C.
点评:熟练掌握两点间的距离公式、点到直线的距离公式、三角形的面积公式、几何概率计算公式是解题的关键.

练习册系列答案
相关题目
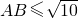 ,则△ABC的面积大于5的概率是
,则△ABC的面积大于5的概率是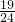


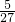
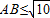 ,则△ABC的面积大于5的概率是( )
,则△ABC的面积大于5的概率是( )