题目内容
【题目】已知A是抛物线E:y2=2px(p>0)上的一点,以点A和点B(2,0)为直径两端点的圆C交直线x=1于M,N两点.
(1)若|MN|=2,求抛物线E的方程;
(2)若0<p<1,抛物线E与圆(x﹣5)2+y2=9在x轴上方的交点为P,Q,点G为PQ的中点,O为坐标原点,求直线OG斜率的取值范围.
【答案】(1)![]() .(2)
.(2)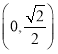
【解析】
(1)设A的坐标为A(x0,y0),由题意可得圆心C的坐标,求出C到直线x=1的距离.由半个弦长,圆心到直线的距离及半径构成直角三角形可得p的值,进而求出抛物线的方程;
(2)将抛物线的方程与圆的方程联立可得韦达定理,进而求出中点G的坐标,再求出直线OG的斜率的表达式,换元可得斜率的取值范围.
(1)设A(x0,y0)且y02=2px0,则圆心C(![]() ),
),
圆C的直径|AB|![]() ,
,
圆心C到直线x=1的距离d=|![]() 1|=|
1|=|![]() |,
|,
因为|MN|=2,所以(![]() )2+d2=(
)2+d2=(![]() )2,即1
)2,即1![]() ,y02=2px0,
,y02=2px0,
整理可得(2p﹣4)x0=0,所以p=2,
所以抛物线的方程为:y2=4x;
(2)联立抛物线与圆的方程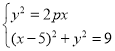 整理可得x2﹣2(5﹣p)x+16=0,△>0,
整理可得x2﹣2(5﹣p)x+16=0,△>0,
设P(x1,y1),Q(x2,y2),则x1+x2=2(5﹣p),x1x2=16,
所以中点G的横坐标xG=5﹣p,yG![]() (
(![]() )
)![]() ,
,
所以kOG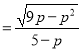 (0<P<1),
(0<P<1),
令t=5﹣p(t∈(4,5)),则kOG![]() (
(![]() ),
),
解得0<kOG![]() ,
,
所以直线OG斜率的取值范围(0,![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目