题目内容
2.已知线段AB,CD分别在两条异面直线上,M,N分别是线段AB,CD的中点,求证:MN<$\frac{1}{2}$(AC+BD)分析 四边形ABCD是空间四边形,而不是平面四边形,要想求MN与AC,BD的关系,必须将它们转化到平面来考虑.
解答 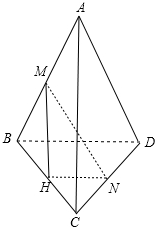 证明:如图所示,取BC中点H,连结MH,NH,MN,
证明:如图所示,取BC中点H,连结MH,NH,MN,
∵M、N分别为AB、CD的中点,
∴MH=$\frac{1}{2}$AC,NH=$\frac{1}{2}$BD,
∵在△HMN中,MH+NH>MN,
∴MN<$\frac{1}{2}$(AC+BD)
点评 本题考查三角形中三边关系的应用,是中档题,解题时要注意三角形中位线定理的合理运用.

练习册系列答案
相关题目
17.直线l与圆x2+y2-4x-4y+7=0相切,且在两坐标轴上的截距相等,这样的直线l有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
12.已知集合A={1,2,3,4,5},B={x|1≤x≤5且x∈R},则A与B的关系是( )
| A. | A?B | B. | A?B | C. | B?A | D. | A=B |