题目内容
已知x,y∈R,且(log23)x+(log35)y≥(log32)y+(log53)x,则x与y应满足( )
| A.x+y≥0 | B.x+y>0 | C.x+y≤0 | D.x+y<0 |
不等式可以变为(log23)x-(log23)-y-[(log53)x-(log53)-y]≥0,
A选项正确,x+y≥0可得x≥-y,由指数函数的性质知(log23)x-(log23)-y是个正数,而(log53)x-(log53)-y是个负数,由此可以判断出(log23)x-(log23)-y-[(log53)x-(log53)-y]≥0.且B选项不对,
C选项不正确,因为由x+y≤0不能确定出(log23)x-(log23)-y的符号,及(log53)x-(log53)-y符号;
同理得D选项不正确.
综上知A选项正确
故选A.
A选项正确,x+y≥0可得x≥-y,由指数函数的性质知(log23)x-(log23)-y是个正数,而(log53)x-(log53)-y是个负数,由此可以判断出(log23)x-(log23)-y-[(log53)x-(log53)-y]≥0.且B选项不对,
C选项不正确,因为由x+y≤0不能确定出(log23)x-(log23)-y的符号,及(log53)x-(log53)-y符号;
同理得D选项不正确.
综上知A选项正确
故选A.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
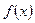 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在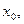 使得
使得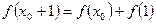 成立,则称函数
成立,则称函数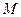 ;反之,若
;反之,若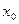 不存在,则称函数
不存在,则称函数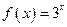 具有性质
具有性质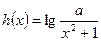 具有性质
具有性质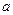 的取值范围
的取值范围