题目内容
如图,圆柱的轴截面 为正方形,
为正方形,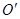 、
、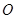 分别为上、下底面的圆心,
分别为上、下底面的圆心, 为上底面圆周上一点,已知
为上底面圆周上一点,已知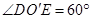 ,圆柱侧面积等于
,圆柱侧面积等于 .
.
(1)求圆柱的体积 ;
;
(2)求异面直线 与
与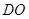 所成角
所成角 的大小.
的大小.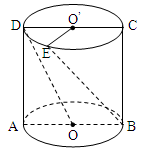
(1)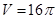 ;(2)
;(2)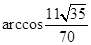 .
.
解析试题分析:(1)了解圆柱的概念,掌握圆柱体积和侧面积计算公式即能解决此题;(2)求异面直线所成角,经常采用平移法,即通过平移,将异面直线所成角转化为相交直线所成角来解决问题,此题可通过平移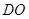 至
至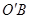 ,转化直线
,转化直线 与
与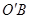 所成角来处理.
所成角来处理.
试题解析:(1)设圆柱的底面半径为 ,由题意,
,由题意, 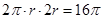
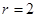 . 2分
. 2分
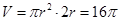 . 6分
. 6分
(2)连接 ,由于
,由于
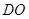 ,
,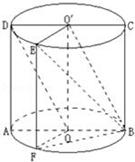

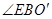 即为异面直线
即为异面直线 与
与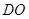 所成角 (或其补角), 8分
所成角 (或其补角), 8分
过点 作圆柱的母线交下底面于点
作圆柱的母线交下底面于点 ,连接
,连接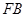 ,
,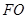
由圆柱的性质,得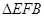 为直角三角形,四边形
为直角三角形,四边形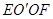 为矩形,
为矩形,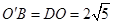 ,
,
由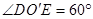 ,由等角定理,得
,由等角定理,得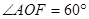 ,所以
,所以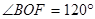 ,可解得
,可解得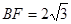 ,
,
在 中,
中,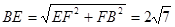 ,
,
由余弦定理,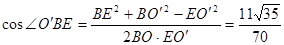 13分
13分 异面直线
异面直线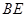 与
与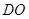 所成角
所成角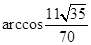 . 14分
. 14分
考点:1.圆柱的体积与表面积;2.异面直线所成角.

练习册系列答案
相关题目
 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.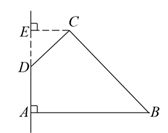
 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,
, 是棱
是棱 的中点。
的中点。 ⊥平面
⊥平面
 ,求几何体
,求几何体 的体积。
的体积。
 及其三视图如图所示,过棱
及其三视图如图所示,过棱 的中点
的中点 作平行于
作平行于 ,
,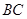 的平面分
的平面分 于点
于点 .
.
 是矩形;
是矩形; 的正弦值.
的正弦值.

 ,则该正方体的表面积为 .
,则该正方体的表面积为 . 角的平面截球O的表面得到圆C.若圆C的面积等于
角的平面截球O的表面得到圆C.若圆C的面积等于 ,则球O的表面积等于 .
,则球O的表面积等于 .