题目内容
18.已知f(x)=ax2-ex(a∈R).(1)当a=1时,令h(x)=f′(x),求h(x)的单调区间;
(2)若x>0时,f(x)有极值点,求实数a的取值范围.
分析 (1)当a=1时,f(x)=x2-ex.令h(x)=f′(x)=2x-ex,h′(x)=2-ex,利用单调性可得ln2是函数h(x)的极大值点,进而得出函数f(x)的单调区间.
(2)f′(x)=2ax-ex,令f′(x)=2ax-ex=0,解得a=$\frac{{e}^{x}}{2x}$=g(x),(x>0).g′(x)=$\frac{{e}^{x}(x-1)}{2{x}^{2}}$,利用单调性即可得出极值,进而得出a的取值范围.
解答 解:(1)当a=1时,f(x)=x2-ex.
令h(x)=f′(x)=2x-ex,
h′(x)=2-ex,当x>ln2时,h′(x)<0,函数h(x)单调递减;当x<ln2时,h′(x)>0,函数h(x)单调递增.
∴ln2是函数h(x)的极大值点,
∴h(x)=f′(x)≤h(ln2)=2ln2-2<0,此时函数f(x)单调递减,函数f(x)无单调递增区间.
(2)f′(x)=2ax-ex,令f′(x)=2ax-ex=0,解得a=$\frac{{e}^{x}}{2x}$=g(x),(x>0).
g′(x)=$\frac{{e}^{x}(x-1)}{2{x}^{2}}$,当x>1时,g′(x)>0,函数g(x)单调递增;当0<x<1时,g′(x)<0,函数g(x)单调递减.
∴当x=1时,函数g(x)取得极小值即最小值,g(1)=$\frac{e}{2}$.
∴$a≥\frac{e}{2}$.
∴实数a的取值范围是$[\frac{e}{2},+∞)$.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了分类讨论方法、推理能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知数列{an}的通项公式为an =n2+1,则该数列的第6项是( )
| A. | 37 | B. | 36 | C. | 26 | D. | 7 |
 如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.
如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.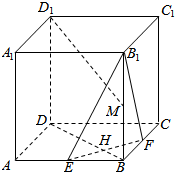 如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:
如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证: