已知an=$\frac{n-4}{n-\frac{9}{2}}$(n∈N+).求数列{an}中的最小项和最大项．题目和参考答案——青夏教育精英家教网—

题目内容

7．已知a_n=$\frac{n-4}{n-\frac{9}{2}}$（n∈N₊），求数列{a_n}中的最小项和最大项．

分析由已知得a_n=1+$\frac{1}{2n-9}$（n∈N₊），由此利用函数性质能求出数列{a_n}中的最小项和最大项．

解答解：∵a_n=$\frac{n-4}{n-\frac{9}{2}}$=$\frac{2n-8}{2n-9}$=1+$\frac{1}{2n-9}$（n∈N₊），
∴n=4时，数列{a_n}取得最小项a₄=1+$\frac{1}{8-9}$=0，
n=5时，数列{a_n}取得最大项a₅=1+$\frac{1}{1}$=2．

点评本题考查数列{a_n}中的最小项和最大项的求法，是基础题，解题时要认真审题，注意数列的函数性质的合理运用．

练习册系列答案

18．设F₁，F₂分别为椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右两个焦点，点$A（1，\;\;\frac{3}{2}）$在椭圆上，且点A到F₁，F₂两点的距离之和等于4．
（1）求椭圆的方程．
（2）若K为椭圆C上的一点，且∠F₁KF₂=30°，求△F₁KF₂的面积．

15．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0．b＞0）上任意一点M（非短轴的端点）与短轴的两个端点 B₁、B₂的连线交x轴于N和K，求证：|ON|•|OK|为定值．

2．将直线l向上平移2个单位后得到直线1₁经过点P（2，2），再将直线l₁绕点P旋转90°后得到的直线l₂过点（4，-2），求直线l的方程．

12．已知恒等式$\frac{sinα}{1+cosα}$=$\frac{1-cosα}{sinα}$就是平方关系sin²α+cos²α=1的一种变形，请你写出利用同角三角函数基本关系的变形而导出的一个恒等式：$\frac{1+sinα}{cosα}=\frac{cosα}{1-sinα}$．

19．在△ABC中，已知b=asinC，c=asinB，试判断△ABC的形状．

17．

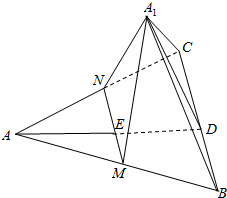如图，AD为△ABC的边BC上的高，E在AD上，且ED=2AE，过E作直线MN∥BC，分别交AB，AC于M，N点，将△AMN沿MN折起到A₁MN，使二面角A₁-MN-C为60°，求证：平面A₁MN⊥平面A₁BC．

18．已知f（x）=ax²-e^x（a∈R）．
（1）当a=1时，令h（x）=f′（x），求h（x）的单调区间；
（2）若x＞0时，f（x）有极值点，求实数a的取值范围．

试题分类