题目内容
设函数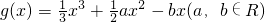 ,在其图象上一点P(x,y)处的切线的斜率记为f(x).
,在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间[-1,3]上是单调递减函数,求a2+b2的最小值.
解:(1)根据导数的几何意义知f(x)=g'(x)=x2+ax-b
由已知-2、4是方程x2+ax-b=0的两个实数
由韦达定理,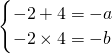 ∴
∴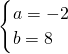 ,f(x)=x2-2x-8(7分)
,f(x)=x2-2x-8(7分)
(2)g(x)在区间[-1,3]上是单调减函数,
所以在[-1,3]区间上恒有f(x)=g'(x)=x2+ax-b≤0,即f(x)=x2+ax-b≤0在[-1,3]恒成立
这只需满足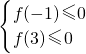 即可,也即
即可,也即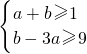
而a2+b2可视为平面区域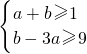 内的点到原点距离的平方,其中点(-2,3)距离原点最近,
内的点到原点距离的平方,其中点(-2,3)距离原点最近,
所以当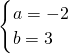 时,a2+b2有最小值13.(14分)
时,a2+b2有最小值13.(14分)
分析:(1)根据导数的几何意义求出f(x)=g'(x),再根据-2、4是方程f(x)=0的两个实数,由韦达定理建立方程组,解之即可;
(2)根据g(x)在区间[-1,3]上是单调减函数,得到函数g(x)在区间[-1,3]上恒有f(x)=g'(x)≤0,然后建立关于a和b的约束条件,而a2+b2可视为平面区域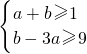 内的点到原点距离的平方,其中点(-2,3)距离原点最近,从而求出a2+b2的最小值.
内的点到原点距离的平方,其中点(-2,3)距离原点最近,从而求出a2+b2的最小值.
点评:本题主要考查了导数的几何意义,以及线性规划的应用等基础知识,考查灵活运用数形结合的思想方法进行探索、分析与解决问题的综合能力,属于中档题.
由已知-2、4是方程x2+ax-b=0的两个实数
由韦达定理,
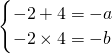 ∴
∴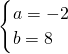 ,f(x)=x2-2x-8(7分)
,f(x)=x2-2x-8(7分)(2)g(x)在区间[-1,3]上是单调减函数,
所以在[-1,3]区间上恒有f(x)=g'(x)=x2+ax-b≤0,即f(x)=x2+ax-b≤0在[-1,3]恒成立
这只需满足
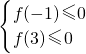 即可,也即
即可,也即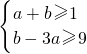
而a2+b2可视为平面区域
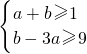 内的点到原点距离的平方,其中点(-2,3)距离原点最近,
内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当
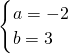 时,a2+b2有最小值13.(14分)
时,a2+b2有最小值13.(14分)分析:(1)根据导数的几何意义求出f(x)=g'(x),再根据-2、4是方程f(x)=0的两个实数,由韦达定理建立方程组,解之即可;
(2)根据g(x)在区间[-1,3]上是单调减函数,得到函数g(x)在区间[-1,3]上恒有f(x)=g'(x)≤0,然后建立关于a和b的约束条件,而a2+b2可视为平面区域
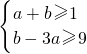 内的点到原点距离的平方,其中点(-2,3)距离原点最近,从而求出a2+b2的最小值.
内的点到原点距离的平方,其中点(-2,3)距离原点最近,从而求出a2+b2的最小值.点评:本题主要考查了导数的几何意义,以及线性规划的应用等基础知识,考查灵活运用数形结合的思想方法进行探索、分析与解决问题的综合能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目