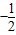题目内容
已知直线y=2x+m和圆 x2+y2=1交于不同的两点A和B,以Ox为始边,OA、OB为终边的角分别为α,β,则sin(α+β)的值为( )
分析:根据题意画出图形,求出tan
=-
,再利用万能公式求出sin(α+β).
| α+β |
| 2 |
| 1 |
| 2 |
解答: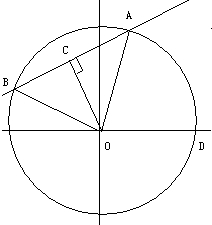 解:如图:过O作OC⊥AB于C点,则OC平分∠AOB
解:如图:过O作OC⊥AB于C点,则OC平分∠AOB
因为以Ox为始边,OA、OB为终边的角分别为α,β,
所以∠AOD=α,∠BOD=β,所以∠COD=
以为OC⊥AB,AB的斜率为:k1=2,所以OC的斜率为:k2=-
,所以 tan
=-
由万能公式得:sin(α+β)=
=-
.
故选B.
 解:如图:过O作OC⊥AB于C点,则OC平分∠AOB
解:如图:过O作OC⊥AB于C点,则OC平分∠AOB因为以Ox为始边,OA、OB为终边的角分别为α,β,
所以∠AOD=α,∠BOD=β,所以∠COD=
| α+β |
| 2 |
以为OC⊥AB,AB的斜率为:k1=2,所以OC的斜率为:k2=-
| 1 |
| 2 |
| α+β |
| 2 |
| 1 |
| 2 |
由万能公式得:sin(α+β)=
2×(-
| ||
1+(-
|
| 4 |
| 5 |
故选B.
点评:本题考查了直线与圆的位置关系,考查直线的斜率,考查万能公式的而运用,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目