题目内容
已知直线y=-2x+m,圆x2+y2+2y=0.
(1)m为何值时,直线与圆相交?
(2)m为何值时,直线与圆相切?
(3)m为何值时,直线与圆相离?
(1)m为何值时,直线与圆相交?
(2)m为何值时,直线与圆相切?
(3)m为何值时,直线与圆相离?
分析:将直线方程与圆联立,结合根的判别式(1)△>0;(2)△=0;(3)△<0,即可求得结论.
解答:解:由
,得5x2-4(m+1)x+m2+2m=0.
△=16(m+1)2-20(m2+2m)=-4[(m+1)2-5],
当△>0时,(m+1)2-5<0,∴-1-
<m<-1+
.
当△=0时,m=-1±
,
当△<0时,m<-1-
或m>-1+
.
故(1)当-1-
<m<-1+
时,直线与圆相交;
(2)当m=-1±
时,直线与圆相切;
(3)当m<-1-
或m>-1+
时,直线与圆相离.
|
△=16(m+1)2-20(m2+2m)=-4[(m+1)2-5],
当△>0时,(m+1)2-5<0,∴-1-
| 5 |
| 5 |
当△=0时,m=-1±
| 5 |
当△<0时,m<-1-
| 5 |
| 5 |
故(1)当-1-
| 5 |
| 5 |
(2)当m=-1±
| 5 |
(3)当m<-1-
| 5 |
| 5 |
点评:本题考查直线与圆的位置关系,考查解不等式,属于中档题.

练习册系列答案
相关题目
已知直线y=2x上一点P的横坐标为a,有两个点A(-1,1),B(3,3),那么使向量
与
夹角为钝角的一个充分不必要条件是( )
| PA |
| PB |
| A、-1<a<2 | ||||||||
| B、0<a<1 | ||||||||
C、-
| ||||||||
| D、0<a<2 |
 已知直线y=2x+k被抛物线x2=4y截得的弦长AB为20,O为坐标原点.
已知直线y=2x+k被抛物线x2=4y截得的弦长AB为20,O为坐标原点.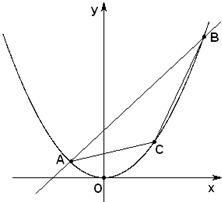 已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.
已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.