Question

4．已知F为抛物线y²=4x的焦点，△ABC的三个顶点都在抛物线上，且$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$．
（1）求|$\overrightarrow{FA}$|+|$\overrightarrow{FB}$|+|$\overrightarrow{FC}$|的值；
（2）设O是坐标原点，记△OFA、△OFB、△OFC的面积分别为S₁、S₂、S₃，判断S₁+S₂+S₃有无最大值，若有，求出最大值；若没有，说明理由．

Answer 1

分析 （1）根据$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$，可判断点F是△ABC重心，进而可求x₁+x₂+x₃的值，再根据抛物线的定义，即可求得答案．
（2）表示出面积，利用y₁+y₂+y₃=0，即可得出结论．

解答 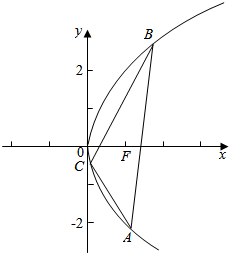解：（1）抛物线焦点坐标F（1，0），准线方程：x=-1
设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃）
∵$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$，
∴点F是△ABC重心，
∴x₁+x₂+x₃=3，
∵|FA|=x₁-（-1）=x₁+1，|FB|=x₂-（-1）=x₂+1，|FC|=x₃-（-1）=x₃+1
∴|$\overrightarrow{FA}$|+|$\overrightarrow{FB}$|+|$\overrightarrow{FC}$|=x₁+1+x₂+1+x₃+1=（x₁+x₂+x₃）+3=3+3=6
（2）如图所示，∵抛物线y²=4x的焦点F的坐标为F（1，0），点F（1，0）是△ABC的重心．
∴S₁=$\frac{1}{2}$|y₁|，S₂=$\frac{1}{2}$|y₂|，S₃=$\frac{1}{2}$|y₃|
∴S₁+S₂+S₃=$\frac{1}{2}$（-y₁+y₂-y₃）=y₂，
∴S₁+S₂+S₃无最大值．

点评 本题重点考查抛物线的简单性质，考查向量知识的运用，解题的关键是判断出F点为三角形的重心．