题目内容
已知有穷数列{an}共有2k项(整数k≥2),首项a1=2,设该数列的前n项和为Sn,且Sn=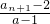 (n=1,2,3,…,2k-1),其中常数a>1.
(n=1,2,3,…,2k-1),其中常数a>1.
(1)求{an}的通项公式;
(2)若a=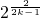 ,数列{bn}满足bn=
,数列{bn}满足bn=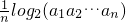 ,(n=1,2,3,…,2k),求证:1≤bn≤2;
,(n=1,2,3,…,2k),求证:1≤bn≤2;
(3)若(2)中数列{bn}满足不等式:|b1- |+
|+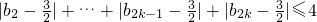 ,求k的最大值.
,求k的最大值.
解:(1)Sn=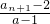 ①,S n+1=
①,S n+1=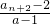 ②
②
②-①得,S n+1-Sn=a n+1=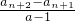
化简整理得,an+2=a•an+1,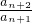 =a( n≥1)
=a( n≥1)
又由已知a1=S1=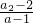 ,整理得出a2=a•a1
,整理得出a2=a•a1
∴数列{an}是以a为公比,以2为首项的等比数列,
通项公式为an=2×a n-1.
(2)由(1)得an=2an-1,
∴a1a2an=2na1+2+…+(n-1)=2n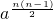 =
= ,
,
bn=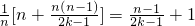 (n=1,2,,2k).
(n=1,2,,2k).
∵2k-1≤n-1∴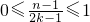
即1≤bn≤2;
(3)设bn≤ ,解得n≤k+
,解得n≤k+ ,又n是正整数,于是当n≤k时,bn<
,又n是正整数,于是当n≤k时,bn< ;
;
当n≥k+1时,bn> .
.
原式=( -b1)+(
-b1)+(  -b2)+…+(
-b2)+…+(  -bk)+(bk+1-
-bk)+(bk+1- )+…+(b2k-
)+…+(b2k- )
)
=(bk+1+…+b2k)-(b1+…+bk)
=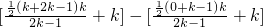 =
=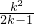 .
.
当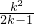 ≤4,得k2-8k+4≤0,4-2
≤4,得k2-8k+4≤0,4-2  ≤k≤4+2
≤k≤4+2  ,又k≥2,
,又k≥2,
∴当k=2,3,4,5,6,7时,原不等式成立.
k的最大值为7.
分析:(1)要根据Sn与an的固有关系an=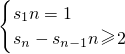 ,得出an+2=a•a n+1,再考虑
,得出an+2=a•a n+1,再考虑 的值,判定{an}的性质去求解.
的值,判定{an}的性质去求解.
(2)首先利用(1)的结论和条件获得an的表达式,然后对a1a2…an进行化简,结合对数运算即可获得数列{bn}的通项公式;
(3)首先利用分类讨论对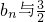 的大小进行判断,然后对所给不等式去绝对值,即可找到关于k的不等式,进而问题即可获得解答.
的大小进行判断,然后对所给不等式去绝对值,即可找到关于k的不等式,进而问题即可获得解答.
点评:本题考查的是数列与不等式的综合类问题.在解答的过程当中充分体现了分类讨论的思想、对数运算的知识以及绝对值和解不等式的知识.值得同学们体会和反思.
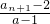 ①,S n+1=
①,S n+1=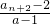 ②
②②-①得,S n+1-Sn=a n+1=
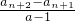
化简整理得,an+2=a•an+1,
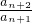 =a( n≥1)
=a( n≥1)又由已知a1=S1=
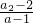 ,整理得出a2=a•a1
,整理得出a2=a•a1∴数列{an}是以a为公比,以2为首项的等比数列,
通项公式为an=2×a n-1.
(2)由(1)得an=2an-1,
∴a1a2an=2na1+2+…+(n-1)=2n
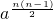 =
= ,
,bn=
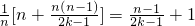 (n=1,2,,2k).
(n=1,2,,2k).∵2k-1≤n-1∴
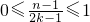
即1≤bn≤2;
(3)设bn≤
 ,解得n≤k+
,解得n≤k+ ,又n是正整数,于是当n≤k时,bn<
,又n是正整数,于是当n≤k时,bn< ;
;当n≥k+1时,bn>
 .
.原式=(
 -b1)+(
-b1)+(  -b2)+…+(
-b2)+…+(  -bk)+(bk+1-
-bk)+(bk+1- )+…+(b2k-
)+…+(b2k- )
)=(bk+1+…+b2k)-(b1+…+bk)
=
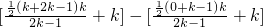 =
=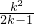 .
.当
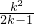 ≤4,得k2-8k+4≤0,4-2
≤4,得k2-8k+4≤0,4-2  ≤k≤4+2
≤k≤4+2  ,又k≥2,
,又k≥2,∴当k=2,3,4,5,6,7时,原不等式成立.
k的最大值为7.
分析:(1)要根据Sn与an的固有关系an=
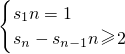 ,得出an+2=a•a n+1,再考虑
,得出an+2=a•a n+1,再考虑 的值,判定{an}的性质去求解.
的值,判定{an}的性质去求解.(2)首先利用(1)的结论和条件获得an的表达式,然后对a1a2…an进行化简,结合对数运算即可获得数列{bn}的通项公式;
(3)首先利用分类讨论对
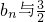 的大小进行判断,然后对所给不等式去绝对值,即可找到关于k的不等式,进而问题即可获得解答.
的大小进行判断,然后对所给不等式去绝对值,即可找到关于k的不等式,进而问题即可获得解答.点评:本题考查的是数列与不等式的综合类问题.在解答的过程当中充分体现了分类讨论的思想、对数运算的知识以及绝对值和解不等式的知识.值得同学们体会和反思.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目