题目内容
已知函数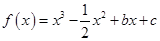 ,且
,且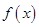 在
在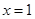 处取得极值.
处取得极值.
(1)求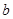 的值;
的值;
(2)若当 时,
时,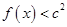 恒成立,求
恒成立,求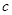 的取值范围;
的取值范围;
(3)对任意的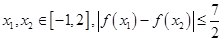 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
【答案】
(1)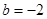 (2)
(2)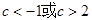 (3)不等式恒成立,证明:当
(3)不等式恒成立,证明:当 时,
时,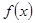 有极小值
有极小值 又
又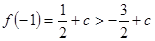 ∴
∴ 时,
时,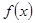 最小值为
最小值为
∴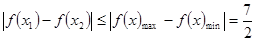 ,故结论成立.
,故结论成立.
【解析】
试题分析:(1)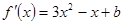
∵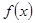 在
在 处取得极值,
处取得极值,
∴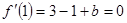
∴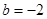 经检验,符合题意.
经检验,符合题意.
(2)∵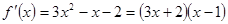
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∴当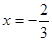 时,
时,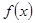 有极大值
有极大值
又
∴ 时,
时,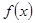 最大值为
最大值为
∴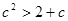 故
故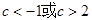
(3)对任意的 恒成立.
恒成立.
由(2)可知,当 时,
时,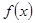 有极小值
有极小值
又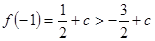
∴ 时,
时,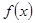 最小值为
最小值为
∴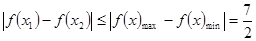 ,故结论成立.
,故结论成立.
考点:导数应用求极值最值
点评:将不等式恒成立问题转化为求函数最值问题是此类题目的最常见的转化思路,需引导学生加以重视

练习册系列答案
相关题目
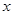
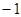
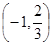

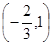

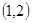
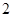
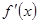
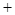


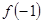



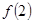
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 在
在 处取得极小值
处取得极小值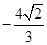 。设
。设 表示
表示 满足:
满足:
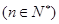
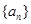 的通项公式
的通项公式 ;
;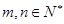 ,若
,若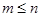 ,证明:
,证明: ;
;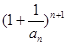 与
与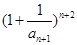 的大小。
的大小。 为奇函数,且
为奇函数,且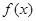 在
在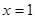 处取得极大值2.
处取得极大值2.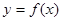 的解析式;
的解析式;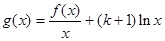 ,求函数
,求函数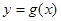 的单调区间。
的单调区间。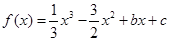 ,且
,且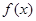 在
在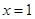 处取得极值.
处取得极值. 的值;
的值;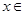 [-1,
[-1,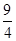 ]时,
]时,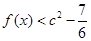 恒成立,求
恒成立,求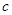 的取值范围.
的取值范围.