题目内容
已知函数![]() ,且在
,且在![]() 处取得极值.
处取得极值.
(1)求b的值;
(2)若对![]() [一1,2]时,
[一1,2]时,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)对任意![]() ∈[一1,2],
∈[一1,2],![]() 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
解:(1)∵![]() ,∴
,∴![]() ,
,
∵![]() 在
在![]() 处取得极值,∴
处取得极值,∴![]() ,∴
,∴![]() .
.
(2)![]() ,∵
,∵![]()
|
|
|
|
| 1 | (1,+∞) |
|
| + | 0 | ― | 0 | + |
|
| ↑ |
| ↓ |
| ↑ |
∴当![]() 时,函数
时,函数![]() 单调递增;当
单调递增;当![]() 时,函数单调递减;
时,函数单调递减;
当![]() ∈(1,2)时,函数
∈(1,2)时,函数![]() 单调递增.
单调递增.
∴当![]() 时,
时,![]() 的极大值
的极大值![]() .
.
又![]() ,
,![]()
∴![]() ∈[一1,2]时,
∈[一1,2]时,![]() 的最大值为
的最大值为![]() ,
,
∴c的取值范围为(一∞,l)∪(2,+∞).
(3)任意的![]() ∈[―1,2],
∈[―1,2],![]() 恒成立.
恒成立.
由(2)知,当![]() 时,
时,![]() 有极小值
有极小值![]() ,又
,又![]()
∴![]() [一1,2]时,
[一1,2]时,![]() 的最小值为
的最小值为![]() .
.
∴当![]() ,故结论成立。
,故结论成立。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
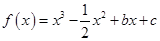 ,且
,且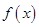 在
在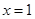 处取得极值.
处取得极值.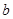 的值;
的值; 时,
时,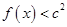 恒成立,求
恒成立,求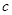 的取值范围;
的取值范围;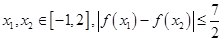 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由. 是定义在
是定义在 上的奇函数,且
上的奇函数,且 在
在 处取得极小值
处取得极小值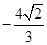 。设
。设 表示
表示 满足:
满足:
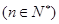
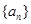 的通项公式
的通项公式 ;
;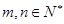 ,若
,若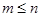 ,证明:
,证明: ;
;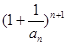 与
与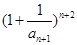 的大小。
的大小。 为奇函数,且
为奇函数,且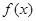 在
在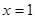 处取得极大值2.
处取得极大值2.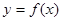 的解析式;
的解析式;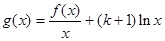 ,求函数
,求函数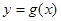 的单调区间。
的单调区间。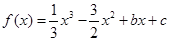 ,且
,且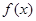 在
在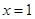 处取得极值.
处取得极值. 的值;
的值;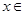 [-1,
[-1,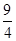 ]时,
]时,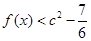 恒成立,求
恒成立,求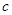 的取值范围.
的取值范围.