题目内容
(08年新建二中模拟文) (12分) 已知![]() 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求| AC |的取值范围.
解析:(1)![]()
依题意![]() 在
在![]() 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴x = 0是f (x)的一个极值点,故![]() ,得c = 0
,得c = 0
(2) 因为f (x)交x轴于点B(2,0)
∴![]() ,即
,即![]()
令![]() 得
得![]()
因为f (x)在[0,2]和[4,5]上有相反的单调性,∴![]() 在[0,2]和[4,5]上有相反的符号
在[0,2]和[4,5]上有相反的符号
故2≤![]() ≤4 Þ -6≤
≤4 Þ -6≤![]() ≤-3
≤-3
假设存在点M(x0,y0)使得f (x)在点M的切线斜率为3b,则f / (x0) =3b,
即![]()
![]()
而-6≤![]() ≤-3,∴△<0
≤-3,∴△<0
故不存在点M(x0,y0),使得f (x)在点M的切线斜率为3b.
(3)解:设![]() ,依题意可令
,依题意可令![]()
![]()
则![]() 即
即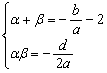
∴![]()
∵-6≤![]() ≤-3,∴当
≤-3,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,故3≤| AC |≤4
,故3≤| AC |≤4![]() .
.

练习册系列答案
相关题目