题目内容
(本小题满分12分) 已知圆 过两点
过两点 ,且圆心
,且圆心 在
在 上.
上.
(1)求圆 的方程;
的方程;
(2)设 是直线
是直线 上的动点,
上的动点, 是圆
是圆 的两条切线,
的两条切线, 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值.
(1) (x-1)2+(y-1)2=4. (2) S=2 =2
=2 =2
=2 .
.
【解析】
试题分析:(1)根据题意,设出圆心(a,b),然后圆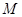 过两点
过两点 ,其中垂线必定过圆心,且圆心
,其中垂线必定过圆心,且圆心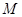 在
在 上.联立直线的方程组得到交点坐标即为圆心坐标,进而两点距离公式求解半径,得到圆的方程。
上.联立直线的方程组得到交点坐标即为圆心坐标,进而两点距离公式求解半径,得到圆的方程。
(2)因为四边形PAMB的面积S=S△PAM+S△PBM= |AM|·|PA|+
|AM|·|PA|+ |BM|·|PB|,根据两个三三角形的底相同,高相等,那么即可知S=2|PA|,只需要求解切线长|PA|的最小值即可。
|BM|·|PB|,根据两个三三角形的底相同,高相等,那么即可知S=2|PA|,只需要求解切线长|PA|的最小值即可。
解:(1)设圆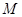 的方程为:(x-a)2+(y-b)2=r2(r>0).
的方程为:(x-a)2+(y-b)2=r2(r>0).
根据题意,得 ﹍﹍﹍﹍﹍﹍﹍3分
﹍﹍﹍﹍﹍﹍﹍3分
解得a=b=1,r=2, ﹍﹍﹍﹍﹍﹍﹍5分
故所求圆M的方程为(x-1)2+(y-1)2=4. ﹍﹍﹍﹍﹍﹍﹍6分
(2)因为四边形PAMB的面积S=S△PAM+S△PBM= |AM|·|PA|+
|AM|·|PA|+ |BM|·|PB|,
|BM|·|PB|,
又|AM|=|BM|=2,|PA|=|PB|, 所以S=2|PA|, ﹍﹍﹍﹍﹍﹍﹍8分而|PA|=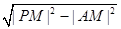 =
= , 即S=2
, 即S=2 .
.
因此要求S的最小值,只需求|PM|的最小值即可,
即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,﹍﹍﹍﹍﹍﹍﹍9分
所以|PM|min= =3,
﹍﹍﹍﹍﹍﹍﹍10分
=3,
﹍﹍﹍﹍﹍﹍﹍10分
所以四边形PAMB面积的最小值为S=2 =2
=2 =2
=2 . ﹍﹍﹍12分
. ﹍﹍﹍12分
考点:本试题主要是考查了圆的方程的求解以及运用切线长和圆的半径和圆心到圆外一点的距离的勾股定理的关系可知,求解四边形面积的最值的问题就是转换为解三角形面积的最值的运用。
点评:结合该试题的关键是理解圆心和半径是求解圆的方程核心,同时直线与圆相切时,构成的四边形的面积问题,能否转化为一条切线和一个半径以及一个圆心到圆外一点P的三角形的面积的最值,最终化简为只需要求解切线长|PA|的最小值即可。。
