题目内容
{xn}是首项为1,公比为
的等比数列,
=(xi,
),(i=1,2,…,n),
=
opi,
=(0,t),若
⊥
,求实数t的取值范围.
| 1 |
| 2 |
| opi |
| 1 |
| xi |
| op |
| n |
 |
| i=1 |
| om |
| op |
| om |
分析:根据向量的坐标运算法则和等比数列求和公式,算出
=
opi=(2-
,2n-1),由
⊥
建立关于t、n的等式,解出t=
,最后根据n∈N*计算分式函数的值域,即可求得实数t的取值范围.
| op |
| n |
 |
| i=1 |
| 1 |
| 2n-1 |
| op |
| om |
| 1 |
| 2n-1 |
解答:解:∵{xn}是首项为1,公比为
的等比数列,
=(xi,
)(i=1,2,…,n),
∴
=
opi=(x1+x2+…+xn,
+
+…+
)
=(1+
+
+…+
,1+2+22+…+2n-1)
=(
,
)=(2-
,2n-1)
∵
⊥
,
=(0,t)
∴(2-
)•0+(2n-1)•t=0,解得t=
∵n∈N*,∴2n-1≥1,可得
∈(0,1],即实数t的取值范围为(0,1].
| 1 |
| 2 |
| opi |
| 1 |
| xi |
∴
| op |
| n |
 |
| i=1 |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
=(1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
=(
1-(
| ||
1-
|
| 1-2n |
| 1-2 |
| 1 |
| 2n-1 |
∵
| op |
| om |
| om |
∴(2-
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
∵n∈N*,∴2n-1≥1,可得
| 1 |
| 2n-1 |
点评:本题着重考查了向量的坐标运算法则、向量数量积公式及其运算性质、等比数列的通项与求和、函数值域的求法等知识,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 (2013•上海)在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.
(2013•上海)在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.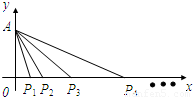 在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.
在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.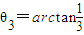 ,求点A的坐标;
,求点A的坐标; ),求θn的最大值及相应n的值.
),求θn的最大值及相应n的值.