题目内容
已知函数f(x)＝ax2＋bx(a＜0)，对于数列{an}，设它的前n项的和为Sn，且Sn＝f(n)(n∈N*)．
(1)证明数列{an}是递减的等差数列；
(2)证明所有的点Mk(k，
)(k∈N*)在同一直线L1上；
(3)设过点(1，a1)、(2，a2)的直线为L2，求L1与L2的夹角的最大值．
答案：
解析：
解析：
|
证明(1)Sn＝an2＋bn，a1＝a＋b an＝sn－sn－1＝(2n－1)a＋b n≥2 当n＝1时也适合． ∴an＝(2n－1)a＋b ∵an－an－1＝2a(定值) ∴数列{an}为等差数列 又∵an－an－1＝2a＜0 即an＜an－1 ∴{an}为递减数列 证明(2)设任意两点Mk(k， 两点斜率 所以所有的点在同一直线y－(a＋b)＝a(x－1)上 (法二，f(k)＝ 解(3)L1方程y＝ax＋b k1＝a N1(1，a＋b) N2(2，3a＋b) k2＝2a tanθ＝ ＝ ∴tanθ≤ ∴θmax＝arc |
)，Mn(n，
) n≠k
＝
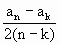＝a(实值)
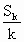＝ak＋b)
＝
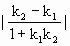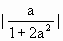(a＜0)
∵|
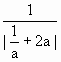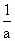＋2a|≥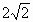
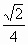当且仅当a＝－
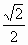时取等号 又tanθ在(0，
)上递增
练习册系列答案
相关题目
)＝
，
在同一周期内有最高点
和最低点
，求此函数的解析式．
恒过点
．
的值；
的最小正周期及单调递减区间．
恒过点
．
的值；
的最小正周期及单调递减区间．