题目内容
如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
| A.288种 | B.264种 | C.240种 | D.168种 |
B
解析试题分析:解
B,D,E,F用四种颜色,则有 种涂色方法;
种涂色方法;
B,D,E,F用三种颜色,则有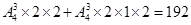 种涂色方法;
种涂色方法;
B,D,E,F用两种颜色,则有 种涂色方法
种涂色方法
根据分类计数原理知共有24+192+48=264种不同的涂色方法,故选B.
考点:排列组合
点评:本题主要考查排列组合的基础知识与分类讨论思想,属于难题.近两年天津卷中的排列、组合问题均处理压轴题的位置,且均考查了分类讨论思想及排列、组合的基本方法,要加强分类讨论思想的训练.

练习册系列答案
相关题目
二项式 的展开式的第二项的系数为
的展开式的第二项的系数为 ,则
,则 的值为( )
的值为( )
A. | B. | C. 或 或 | D. 或 或 |
某中学从 名男生和
名男生和 名女生中推荐
名女生中推荐 人参加社会公益活动,若选出的
人参加社会公益活动,若选出的 人中既有男生又有女生,则不同的选法共有( )
人中既有男生又有女生,则不同的选法共有( )
A. 种 种 | B. 种 种 | C. 种 种 | D.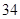 种 种 |
某城市的街道如图,某人要从A地前往B地,则路程最短的走法有
| A.8种 | B.10种 | C.12种 | D.32种 |
四名同学争夺跑步、跳高、跳远三项冠军,则可能的结果数是( )
A. | B. | C. | D. |
已知等式
 ,则
,则 的值分别为
的值分别为
A. | B. | C. | D. |
在航天员进行的一项太空实验中,要先后实施6个程序,其中程序A只能出现在第一或最后一步,程序B和C在实施时必须相邻,问实验顺序的编排方法共有
| A.96种 | B.48种 | C.34种 | D.144种 |
从6人中选4人分别到北京、哈尔滨、广州、成都四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且在这6人中甲、乙不去哈尔滨游览,则不同的选择方案共有
| A.300种 | B.240种 | C.144种 | D.96种 |
设函数 , 则当x>0时,
, 则当x>0时,  表达式的展开式中常数项为 ( )
表达式的展开式中常数项为 ( )
| A.-20 | B.20 | C.-15 | D.15 |