题目内容
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3) 现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
(1)A班学生的视力较好;(2)B班5名学生视力的方差较大;(3)所以随机变量 的分布列如下:
的分布列如下:
0 1 2 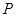
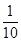
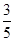
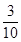
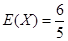 .
.
解析试题分析:(1)计算出平均数,看平均数的大小,平均数大的班学生的视力较好;(2)对数据分析,一看极差,二看数据集中程度,越集中方差越小,越离散方差越大,从数据上看,B班5名学生视力极差较大,数据相对较散,从而的结论;(3)对数据观察,找出视力大于4.6的人数,从而确定出 的所有可能取值,分别求出它们的概率,得分布列,进而可求出期望.
的所有可能取值,分别求出它们的概率,得分布列,进而可求出期望.
(1) A班5名学生的视力平均数为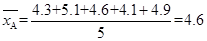 , 2分
, 2分
B班5名学生的视力平均数为 . 3分
. 3分
从数据结果来看A班学生的视力较好. 4分
(2)B班5名学生视力的方差较大. 7分
(3)由(1)知,A班的5名学生中有2名学生视力大于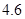 .
.
则 的所有可能取值为
的所有可能取值为 ,
,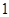 ,
, . 8分
. 8分
所以 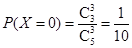 ; 9分
; 9分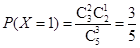 ; 10分
; 10分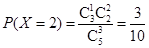 . 11分
. 11分
所以随机变量 的分布列如下:
的分布列如下:
12分
0 1 2 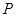
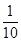
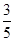
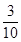
故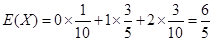 . 13分
. 13分
考点:统计数据分析,平均数,方差,分布列与期望.

学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(1)求表格中
 与
与 的值;
的值;(2)从被检测的
 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率. 

 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
. ,
, 的值;
的值;
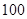 名年龄段在
名年龄段在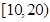 ,
,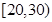 ,
,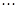 ,
,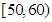 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示. 的人数;
的人数; 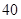 岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取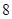 人,求
人,求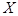 为年龄在
为年龄在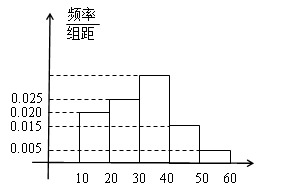

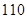 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的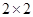 列联表,如表2.
列联表,如表2.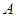 、
、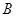 、
、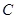 、
、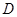 、
、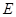 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关; 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.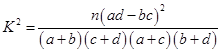 ,其中
,其中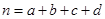 .
.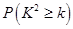
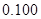
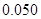
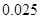
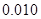
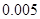
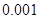
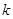
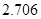
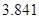

 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在 的分布列及数学期望.
的分布列及数学期望.