题目内容
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为ξ,求ξ的分布列及数学期望.
【答案】分析:(1)设事件A1表示甲选22题,A2表示甲选23题,A3表示甲选24题,B1表示乙选22题,B2表示乙选23题,B3表示乙选24题,则甲、乙两人选做同一题事件为A1B1+A2B2+A3B3,根据独立事件概率乘法公式,可得答案.
(2)ξ可能取值为0,1,2,3,4,5.结合5名考生选做这三题的任意一题的可能性均为 ,可计算出ξ的分布列及数学期望
,可计算出ξ的分布列及数学期望
解答:解:(1)设事件A1表示甲选22题,A2表示甲选23题,A3表示甲选24题,
B1表示乙选22题,B2表示乙选23题,B3表示乙选24题,
则甲、乙两人选做同一题事件为A1B1+A2B2+A3B3,
且A1与B1,A2与B2,A3与B3相互独立,
所以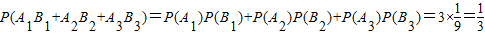 …(4分)
…(4分)
(2)ξ可能取值为0,1,2,3,4,5.
且5名考生选做这三题的任意一题的可能性均为 ,
,
∴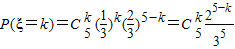 ,k=0,1,2,3,4,5
,k=0,1,2,3,4,5
∴分布列为
∴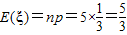 …(12分)
…(12分)
点评:此题考查了离散型随机变量的定义及其分布列,并且利用分布列求出期望,还考查了考虑问题时的严谨的逻辑思维及计算能力.
(2)ξ可能取值为0,1,2,3,4,5.结合5名考生选做这三题的任意一题的可能性均为
 ,可计算出ξ的分布列及数学期望
,可计算出ξ的分布列及数学期望解答:解:(1)设事件A1表示甲选22题,A2表示甲选23题,A3表示甲选24题,
B1表示乙选22题,B2表示乙选23题,B3表示乙选24题,
则甲、乙两人选做同一题事件为A1B1+A2B2+A3B3,
且A1与B1,A2与B2,A3与B3相互独立,
所以
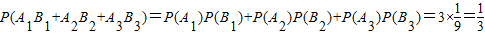 …(4分)
…(4分)(2)ξ可能取值为0,1,2,3,4,5.
且5名考生选做这三题的任意一题的可能性均为
 ,
,∴
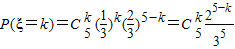 ,k=0,1,2,3,4,5
,k=0,1,2,3,4,5∴分布列为
| ξ | 1 | 2 | 3 | 4 | 5 | |
| P | 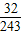 | 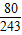 | 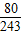 | 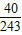 | 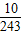 | 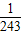 |
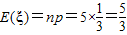 …(12分)
…(12分)点评:此题考查了离散型随机变量的定义及其分布列,并且利用分布列求出期望,还考查了考虑问题时的严谨的逻辑思维及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
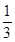 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.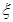 ,求
,求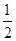 .
.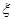 ,求
,求