题目内容
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为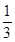 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为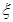 ,求
,求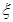 的分布列及数学期望.
的分布列及数学期望.
【答案】
(1)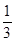 ;(2)
;(2)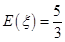 .
.
【解析】
试题分析:(1) 设事件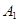 表示甲选22题,
表示甲选22题, 表示甲选23题,
表示甲选23题,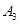 表示甲选24题,
表示甲选24题,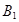 表示乙选22题,
表示乙选22题,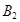 表示乙选23题,
表示乙选23题,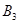 表示乙选24题,则甲、乙两人选做同一题事件为
表示乙选24题,则甲、乙两人选做同一题事件为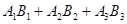 ,且
,且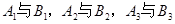 相互独立,根据相互独立事件概率的求法计算可得;(2)
相互独立,根据相互独立事件概率的求法计算可得;(2)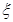 服从二项分布,根据二项分布概率的计算方法可列出分布列.
服从二项分布,根据二项分布概率的计算方法可列出分布列.
试题解析:(1)设事件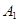 表示甲选22题,
表示甲选22题, 表示甲选23题,
表示甲选23题,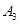 表示甲选24题,
表示甲选24题,
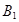 表示乙选22题,
表示乙选22题,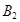 表示乙选23题,
表示乙选23题,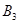 表示乙选24题,
表示乙选24题,
则甲、乙两人选做同一题事件为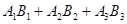 ,且
,且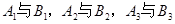 相互独立,
相互独立,
所以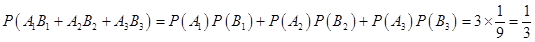 4分
4分
(2)设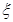 可能取值为0,1,2,3,4,5.
可能取值为0,1,2,3,4,5.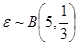
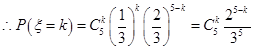 ,
,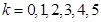
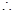 分布列为
分布列为
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
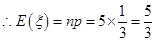 12分
12分
考点:1.相互独立事件概率的计算;2.二项分布的分布列和数学期望.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
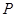
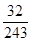
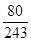
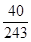
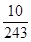
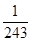
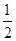 .
.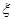 ,求
,求