题目内容

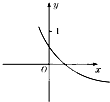已知函数f（x）=log_a（3^x+b-1）（a＞0，a≠1）的图象如图所示，则a，b满足的关系是

A.
0＜a＜b＜1
B.
0＜b＜a＜1
C.
0＜a＜1＜b
D.
0＜b＜1＜a

A
分析：由图象可知对数的底数满足0＜a＜1，且0＜f（0）＜1．
解答：由图象可知0＜a＜1且0＜f（0）＜1
即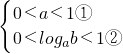 $\text{[math]}$
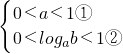
解②得log_a1＜log_ab＜log_aa
∵0＜a＜1∴由对数函数的单调性可知a＜b＜1
结合①可得a，b满足的关系为0＜a＜b＜1
故选A．
点评：本题主要考查了对数函数的图象与性质以及对图形语言的认知转化的能力．

练习册系列答案

黄冈状元成才路暑假作业新疆人民出版社系列答案

暑假特训浙江大学出版社系列答案

名师一号假期作业暑假作业河北教育出版社系列答案

第三学期赢在暑假系列答案

暑假作业宁夏人民教育出版社系列答案

优化学习暑假40天江苏人民出版社系列答案

快乐暑假学段衔接提升方案新疆美术摄影出版社系列答案

假期作业济南出版社系列答案

快乐假期暑假生活延边人民出版社系列答案

学练快车道快乐假期暑假作业新疆人民出版社系列答案

相关题目

已知函数f（x）=2x-2+ae^-x（a∈R）
（1）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求a的值；
（2）当a=1时，若直线l：y=kx-2与曲线y=f（x）在（-∞，0）上有公共点，求k的取值范围．

已知函数f（x）=x²+2|lnx-1|．
（1）求函数y=f（x）的最小值；
（2）证明：对任意x∈[1，+∞），lnx≥

恒成立；
（3）对于函数f（x）图象上的不同两点A（x₁，y₁），B（x₂，y₂）（x₁＜x₂），如果在函数f（x）图象上存在点M（x₀，y₀）（其中x₀∈（x₁，x₂））使得点M处的切线l∥AB，则称直线AB存在“伴侣切线”．特别地，当x₀=

时，又称直线AB存在“中值伴侣切线”．试问：当x≥e时，对于函数f（x）图象上不同两点A、B，直线AB是否存在“中值伴侣切线”？证明你的结论．

已知函数f（x）=x²-bx的图象在点A（1，f（1））处的切线l与直线x+3y-1=0垂直，若数列{

}的前n项和为S_n，则S₂₀₁₂的值为（　　）

已知函数f（x）=xlnx
（Ⅰ）求函数f（x）的极值点；
（Ⅱ）若直线l过点（0，-1），并且与曲线y=f（x）相切，求直线l的方程．

已知函数f（x）=

，a≠0且a≠1．
（1）试就实数a的不同取值，写出该函数的单调增区间；
（2）已知当x＞0时，函数在（0，

）上单调递减，在（

，+∞）上单调递增，求a的值并写出函数的解析式；
（3）记（2）中的函数图象为曲线C，试问是否存在经过原点的直线l，使得l为曲线C的对称轴？若存在，求出直线l的方程；若不存在，请说明理由．