题目内容
已知圆M:(x+| 3 |
| 2 |
| 9r2 |
| 4 |
| PQ |
| QN |
| 1 |
| 2 |
(1)求点Q的轨迹方程;
(2)若点Q对应曲线与x轴两交点为A,B,点R是该曲线上一动点,曲线在R点处的切线与在A,B两点处的切线分别交于C,D两点,求AD与BC交点S的轨迹方程.
分析:(1)设点Q的坐标为(x,y),由题设条件求出点P的坐标为(
,
y),代入圆M的方程化简就能得到所求点Q的轨迹方程.
(2)设点R的坐标为(x0,y0)(y0≠0),则x02+y02=r2.由题设条件可求得C、D两点的坐标为C(-r,
) ,D(r,
),
再由直线BC、AD的方程分别为y=
(x-r),y=
(x+r),两式相乘,得y2=
(x2-r2),化简就能得到所求点S的轨迹方程.
| 3(x-r) |
| 2 |
| 3 |
| 2 |
(2)设点R的坐标为(x0,y0)(y0≠0),则x02+y02=r2.由题设条件可求得C、D两点的坐标为C(-r,
| r2+x0r |
| y0 |
| r2-x0r |
| y0 |
再由直线BC、AD的方程分别为y=
| r2+x0r |
| -2r2y02 |
| r2-x0r |
| 2ry0 |
| r2(r2-x02) |
| -4r2y02 |
解答:解:(1)设点Q的坐标为(x,y),∵
=
,N(3r,0),
∴点P的坐标为(
,
y),代入圆M的方程化简得x2+y2=r2即为所求点Q的轨迹方程.
(2)设点R的坐标为(x0,y0)(y0≠0),则x02+y02=r2.
圆在R点处的切线方程为:x0x+y0y=r2.
又切线AC、BD的方程分别为x=-r,x=r,
解方程组可得C、D两点的坐标为C(-r,
) ,D(r,
),
∴直线BC、AD的方程分别为y=
(x-r),y=
(x+r),
两式相乘,得y2=
(x2-r2),化简得x2+4y2=r2(y≠0).
∴所求点S的轨迹方程为x2+4y2=r2(y≠0).
| PQ |
| QN |
| 1 |
| 2 |
∴点P的坐标为(
| 3(x-r) |
| 2 |
| 3 |
| 2 |
(2)设点R的坐标为(x0,y0)(y0≠0),则x02+y02=r2.
圆在R点处的切线方程为:x0x+y0y=r2.
又切线AC、BD的方程分别为x=-r,x=r,
解方程组可得C、D两点的坐标为C(-r,
| r2+x0r |
| y0 |
| r2-x0r |
| y0 |
∴直线BC、AD的方程分别为y=
| r2+x0r |
| -2r2y02 |
| r2-x0r |
| 2ry0 |
两式相乘,得y2=
| r2(r2-x02) |
| -4r2y02 |
∴所求点S的轨迹方程为x2+4y2=r2(y≠0).
点评:本题考查轨迹方程,有一定的难度,解题时要认真审题,注意挖掘题设中的隐含条件,耐心寻找数量间的相互关系,注意公式的灵活运用.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
 (2010•重庆三模)如图,已知圆G:
(2010•重庆三模)如图,已知圆G: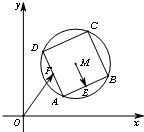 (2013•丽水一模)如图,已知圆M:(x-3)2+(y-3)2=4,四边形 ABCD为圆M的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心M转动时,
(2013•丽水一模)如图,已知圆M:(x-3)2+(y-3)2=4,四边形 ABCD为圆M的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心M转动时,