题目内容
4.在△ABC中,内角A,B,C的所对边分别是a,b,c,有如下下列命题:①若A>B>C,则sinA>sinB>sinC;
②若$\frac{cosA}{a}=\frac{cosB}{b}=\frac{cosC}{c}$,则△ABC为等边三角形;
③若sin2A=sin2B,则△ABC为等腰三角形;
④若(1+tanA)(1+tanB)=2,则△ABC为钝角三角形;
⑤存在A,B,C,使得tanAtanBtanC<tanA+tanB+tanC成立.
其中正确的命题为①②④(写出所有正确命题的序号)
分析 ①已知不等式利用正弦定理化简,整理得到结果,即可做出判断;
②已知等式利用正弦定理化简,整理得到结果,即可做出判断;
③已知等式利用正弦函数的性质化简,整理得到结果,即可做出判断;
④已知等式整理后,利用两角和与差的正切函数公式化简,求出C的度数,即可做出判断;
⑤由A,B,C为三角形内角,得到tan(A+B)=tan(π-C)=-tanC,利用两角和与差的正切函数公式化简,整理得到tanA+tanB+tanC=tanAtanBtanC,故本选项错误.
解答 解:①∵A>B>C,
∴a>b>c,
又$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,
∴sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,2R为定值,
∴sinA>sinB>sinC,此选项正确;
②∵$\frac{cosA}{a}$=$\frac{cosB}{b}$=$\frac{cosC}{c}$,
由正弦定理得:a=2R•sinA,b=2R•sinB,c=2R•sinC代入,得$\frac{cosA}{sinA}$=$\frac{cosB}{sinB}$=$\frac{cosC}{sinC}$,
∴$\frac{sinA}{cosA}$=$\frac{sinB}{cosB}$=$\frac{sinC}{cosC}$,即tanA=tanB=tanC,
∴A=B=C,
则△ABC是等边三角形,本选项正确;
③∵sin2A=sin2B,
∴2A=2B或2A+2B=π,
即A=B或A+B=$\frac{π}{2}$,
则△ABC为等腰三角形或直角三角形,本选项错误;
④∵(1+tanA)(1+tanB)=2,即1+tanA+tanB+tanAtanB=2,
∴tanA+tanB+tanAtanB=1,即tanA+tanB=1-tanAtanB,
∴$\frac{tanA+tanB}{1-tanAtanB}$=1,即tan(A+B)=1,
∴A+B=$\frac{π}{4}$,即C=$\frac{3π}{4}$,
则△ABC为钝角三角形,本选项正确;
⑤若A、B、C有一个为直角时不成立,
若A、B、C都不为直角,
∵A+B=π-C,
∴tan(A+B)=tan(π-C),即$\frac{tanA+tanB}{1-tanAtanB}$=-tanC,
则tanA+tanB=-tanC+tanAtanBtanC,
∴tanA+tanB+tanC=tanAtanBtanC,
即⑤错误,
故答案为:①②④
点评 此题考查了同角三角函数间的基本关系,正弦定理,两角和与差的正切函数公式,熟练掌握基本关系是解本题的关键.

| A. | (-∞,$\frac{1}{e}$) | B. | (0,$\frac{1}{e}$) | C. | ($\frac{1}{e}$,+∞) | D. | (-∞,1) |
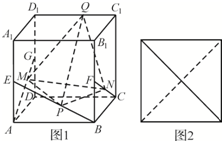 如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点P到QMN的距离为$\frac{\sqrt{3}}{3}$a.
如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点P到QMN的距离为$\frac{\sqrt{3}}{3}$a.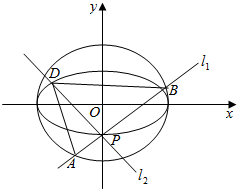 如图,点P(0,-1)是椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
如图,点P(0,-1)是椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.