题目内容
若直角坐标平面内不同的两点P、Q满足条件:①P、Q都在函数f(x)=
y=f(x)的图象上
②P,Q关于原点对称,则称点对[P,Q]是函数Y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).若函数,则此函数的“友好点对”有( )对.
|
②P,Q关于原点对称,则称点对[P,Q]是函数Y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).若函数,则此函数的“友好点对”有( )对.
分析:根据题意:“友好点对”,可知,欲求f(x)的“友好点对”,只须作出函数y=-x2-4x(x≤0)的图象关于原点对称的图象,看它与函数f(x)=log2x,(x>0)交点个数即可.
解答:解:根据题意:当x>0时,-x<0,
则f(-x)=-(-x)2-4(-x)=-x2+4x,
则函数y=-x2-4x(x≤0)的图象关于原点对称的函数是y=x2-4x(x≥0)
由题意知,作出函数y=x2-4x(x≥0)的图象及函数f(x)=log2x,(x>0)的图象如下图所示
由图可得两个函数图象共有两个交点,
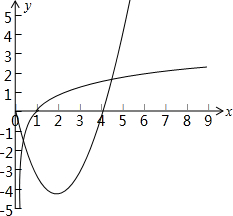
即函数f(x)的“友好点对”有2对,
故选C.
则f(-x)=-(-x)2-4(-x)=-x2+4x,
则函数y=-x2-4x(x≤0)的图象关于原点对称的函数是y=x2-4x(x≥0)
由题意知,作出函数y=x2-4x(x≥0)的图象及函数f(x)=log2x,(x>0)的图象如下图所示
由图可得两个函数图象共有两个交点,

即函数f(x)的“友好点对”有2对,
故选C.
点评:本题考查了奇偶函数图象的对称性,体现了数形结合思想,解答的关键是对“友好点对”的理解,合理的利用图象解决.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
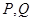 满足条件:①
满足条件:①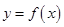 的图像上;②
的图像上;②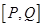 是函数
是函数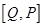 看作同一对“友好点对”).若函数
看作同一对“友好点对”).若函数 ,则此函数的“友好点对”有(
)对.
,则此函数的“友好点对”有(
)对.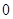 B.
B.
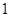 C.
C. D.
D.