题目内容
(2008•江苏二模)设点F1,F2分别为椭圆
+
=1(a>b>0)的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是
| x2 |
| a2 |
| y2 |
| b2 |
[
-1,1)
| 2 |
[
-1,1)
.| 2 |
分析:欲求椭圆离心率e的取值范围,关键是建立a,c之间的不等关系,设M(x,y)利用MF₁,MF₂,d成等比数列,得出
=
,由于M在椭圆上,故-a≤x≤a,即有-1≤x/a≤1,从而得到不等关系-1≤
≤1;解之即可得到e的取值范围.
| x |
| a |
| e-1 |
| e(e+1) |
| e-1 |
| e(e+1) |
解答:解:设M(x,y);l为右准线;
故MF₂=r₂=a-ex; MF₁=r₁=2a-r₂=2a-(a-ex)=a+ex;
MF₁,MF₂,d成等比数列,故有:r2₂=dr₁,
即有(a-ex)2=(a+ex)(a-ex)/e,
化简得e(a-ex)=a+ex,故
=
,
由于M在椭圆上,故-a≤x≤a,即有-1≤x/a≤1,
∴-1≤
≤1;由于e-1<0,
故只需考虑不等式的左边,即考虑-1≤
,-e(e+1)≤e-1,
∴e2+2e-1≧0,故得e≥
-1,
即e的取值范围为[
-1,1).
故答案为:[
-1,1).
故MF₂=r₂=a-ex; MF₁=r₁=2a-r₂=2a-(a-ex)=a+ex;
MF₁,MF₂,d成等比数列,故有:r2₂=dr₁,
即有(a-ex)2=(a+ex)(a-ex)/e,
化简得e(a-ex)=a+ex,故
| x |
| a |
| e-1 |
| e(e+1) |
由于M在椭圆上,故-a≤x≤a,即有-1≤x/a≤1,
∴-1≤
| e-1 |
| e(e+1) |
故只需考虑不等式的左边,即考虑-1≤
| e-1 |
| e(e+1) |
∴e2+2e-1≧0,故得e≥
| 2 |
即e的取值范围为[
| 2 |
故答案为:[
| 2 |
点评:本小题主要考查椭圆的简单性质、等比数列的性质、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
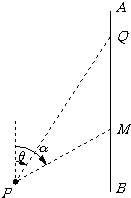 (2008•江苏二模)如图,AB是沿太湖南北方向道路,P为太湖中观光岛屿,Q为停车场,PQ=5.2km.某旅游团游览完岛屿后,乘游船回停车场Q,已知游船以13km/h的速度沿方位角θ的方向行驶,
(2008•江苏二模)如图,AB是沿太湖南北方向道路,P为太湖中观光岛屿,Q为停车场,PQ=5.2km.某旅游团游览完岛屿后,乘游船回停车场Q,已知游船以13km/h的速度沿方位角θ的方向行驶, (2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.
(2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.