Question

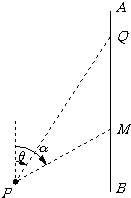（2008•江苏二模）如图，AB是沿太湖南北方向道路，P为太湖中观光岛屿，Q为停车场，PQ=5.2km．某旅游团游览完岛屿后，乘游船回停车场Q，已知游船以13km/h的速度沿方位角θ的方向行驶，sinθ=

5

13

．游船离开观光岛屿3分钟后，因事耽搁没有来得及登上游船的游客甲为了及时赶到停车地点Q与旅游团会合，立即决定租用小船先到达湖滨大道M处，然后乘出租汽车到点Q（设游客甲到达湖滨大道后能立即乘到出租车）．假设游客甲乘小船行驶的方位角是α，出租汽车的速度为66km/h．
（Ⅰ）设sinα=

4

5

，问小船的速度为多少km/h时，游客甲才能和游船同时到达点Q；
（Ⅱ）设小船速度为10km/h，请你替该游客设计小船行驶的方位角α，当角α余弦值的大小是多少时，游客甲能按计划以最短时间到达Q．

Answer 1

分析：（I）作PN⊥AB，N为垂足，由sinθ=

5

13

．sinα=

4

5

，解Rt△PNQ和Rt△PNM，得到PQ和PM及MQ的长，构造方程可得满足条件的船速
（II）当小船行驶的方位角为α时，解三角形分别求出PM，MQ长，进而求出时间t的解析式，利用导数法，求出函数的最小值，可得答案．

解答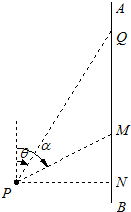：解：（Ⅰ） 如图，作PN⊥AB，N为垂足．
sinθ=

5

13

，sinα=

4

5

，
在Rt△PNQ中，PN=PQsinθ=5.2×

5

13

=2（km），
QN=PQcosθ=5.2×

12

13

=4.8（km）．
在Rt△PNM中，MN=

PN

tanα

=

2

4 3

=1.5（km）．…（3分）
设游船从P到Q所用时间为t₁h，游客甲从P经M到Q所用时间为t₂h，
小船的速度为v₁km/h，则t1=

PQ

13

=

26 5

13

=

2

5

（h），t2=

PM

v1

+

MQ

66

=

2.5

v1

+

3.3

66

=

5

2v1

+

1

20

（h）．  …（5分）
由已知得：t2+

1

20

=t1，

5

2v1

+

1

20

+

1

20

=

2

5

，
∴v1=

25

3

．…（7分）
∴小船的速度为

25

3

km/h时，游客甲才能和游船同时到达Q．
（Ⅱ）在Rt△PMN中，PM=

PN

sinα

=

2

sinα

（km），
MN=

PN

tanα

=

2cosα

sinα

（km）．
∴QM=QN-MN=4.8-

2cosα

sinα

（km）．               …（9分）
∴t=

PM

10

+

QM

66

=

1

5sinα

+

4

55

-

cosα

33sinα

=

1

165

×

33-5cosα

sinα

+

4

55

．…（11分）
∵t′=

1

165

×

5sin2α-(33-5cosα)cosα

sin2α

=

5-33cosα

165sin2α

，…（13分）
∴令t'=0得：cosα=

5

33

．
当cosα＜

5

33

时，t'＞0；当cosα＞

5

33

时，t'＜0．
∵cosα在α∈(0，

π

2

)上是减函数，
∴当方位角α满足cosα=

5

33

时，t最小，
即游客甲能按计划以最短时间到达Q．…（15分）

点评：本题考查的知识点是函数模型的选择与应用，根据已知构造出恰当的函数是解答本题的关键．